
Active contours, or snakes are often used in computer vision and image analysis to detect and locate objects, and to describe their shape. (Its 3D version is often known as deformable models or active surfaces in literature.) For example, a snake might be used to automatically find a manufactured part on an assembly line; one might be used to find the outline of an organ in a medical image; or one might be used to automatically identify characters on a postal letter.
We have developed a kind of snake that permits the snake to start far from the object, and yet still draws it towards the object, and forces it into boundary concavities. The snake is based on a new type of external force field, called gradient vector flow, or GVF. This field is computed as a spatial diffusion of the gradient of an edge map derived from the image. This computation causes diffuse forces to exist far from the object, and crisp force vectors near the edges. Combining these forces with the usual internal forces yields a powerful computational object: the GVF snake (2D), or the GVF deformable model (N-D).
Our snake solves two key problems. These problems are that snakes cannot move toward objects that are too far away and that snakes cannot move into boundary concavities or indentations. Previous efforts to solve these problems have not been completely successful, and have often created new problems along with the proposed solutions.
Our snake, which we call the gradient vector flow (GVF) snake, begins with the calculation of a field of forces, called the GVF forces, over the image domain. The GVF forces are used to drive the snake, modeled as a physical object having a resistance to both stretching and bending, towards the boundaries of the object. The GVF forces are calculated by applying generalized diffusion equations to both components of the gradient of an image edge map

The GVF forces are derived from a diffusion operation, they tend to extend very far away from the object. This extends the "capture range" so that snakes can find objects that are quite far away from the snake's initial position. This same diffusion creates forces which can pull active contours into concave regions. A fundamental difference between this formulation and the traditional formulation is that GVF forces are not purely irrotational (curl-free) forces. In fact, they typically comprise both irrotational and solenoidal (divergence-free) fields. Because of this property, they cannot be derived from the energy minimization framework of traditional snakes.
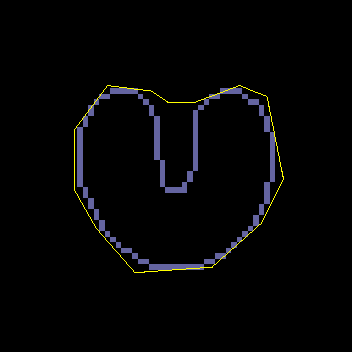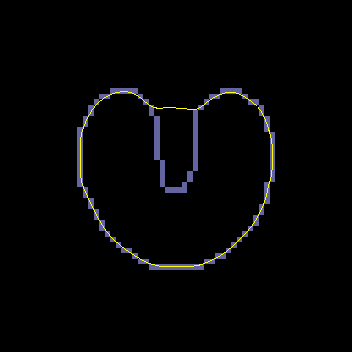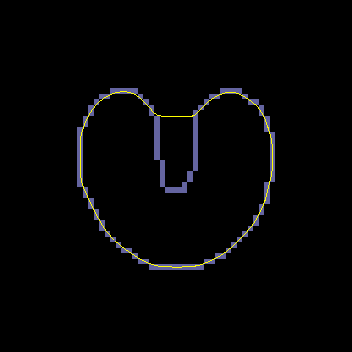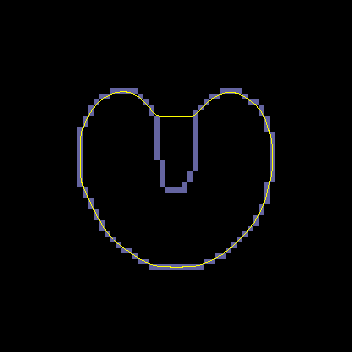
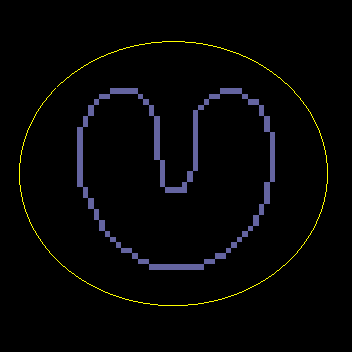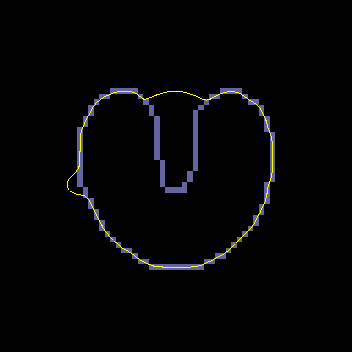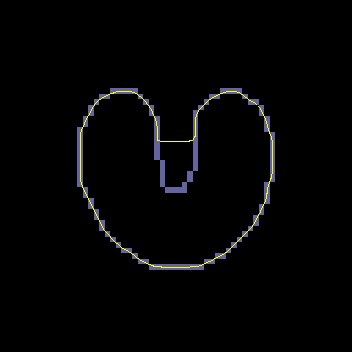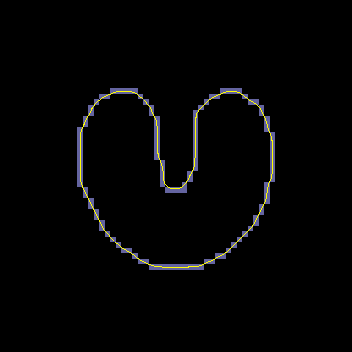
A GVF snake can start far from the boundary and will converge to boundary concavities.
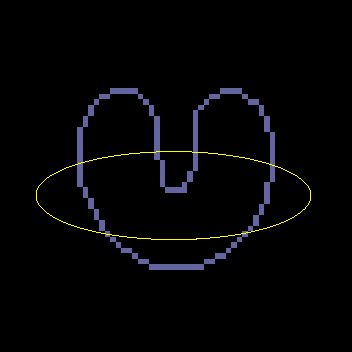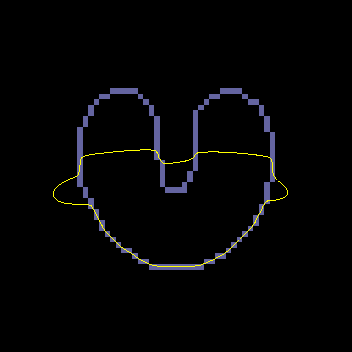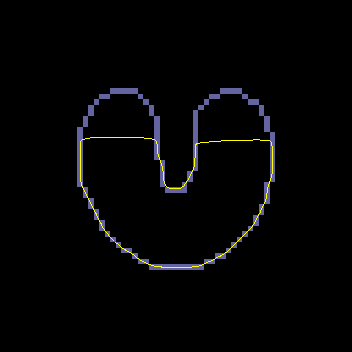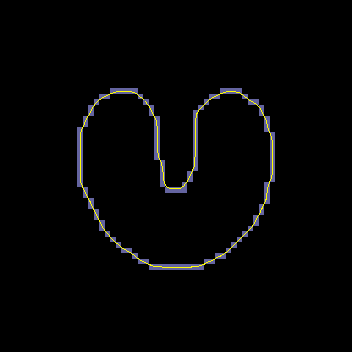
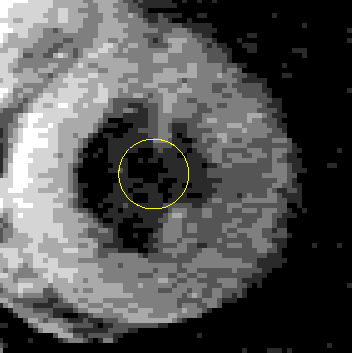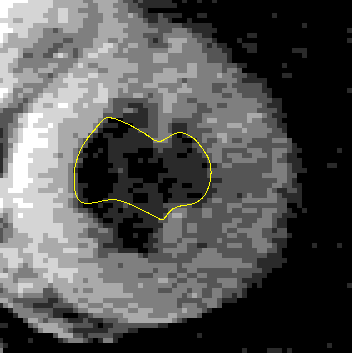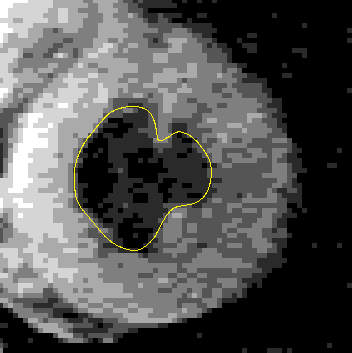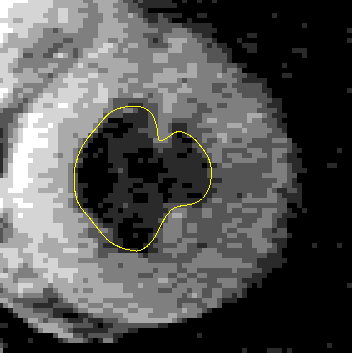
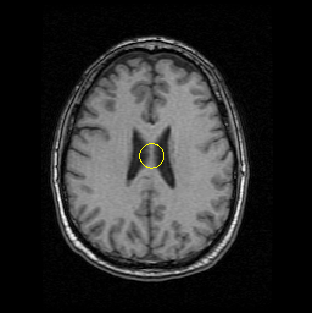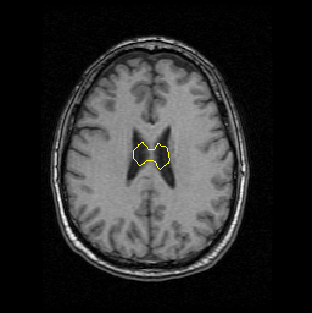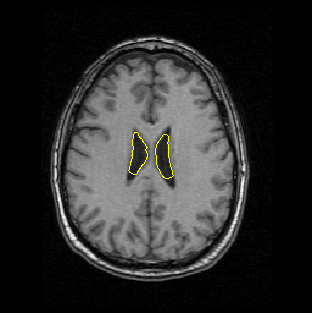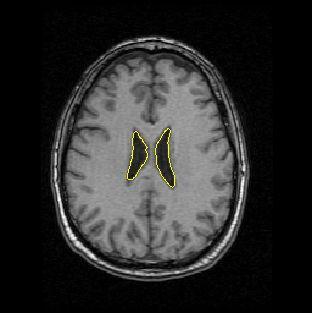
The GVF snake is a new approach to active contours and surfaces. It focuses on the design of the external force first, and the implementation of the snake second. The computations are straightforward, i.e., the diffusion equations are simple to calculate (see publications and software below), and the result is always better than the traditional snake. As outlined in our publications, the GVF usually offers advantages over balloons and distance-based snakes as well. We anticipate and encourage widespread use of the GVF snake and the easily implemented GVF active surface as well. This new approach offers new areas for further improvement as well. For example, we have recently implemented a more general version of GVF, generalized GVF, which offers advantages when the boundary concavity is very thin.