Digitális képfeldolgozás (2012-2013-2)
2. kötelező program lista
Követelmények
A kötelező programot MATLAB-ban kell megvalósítani. A programot egy függvényként kell megírni,
a függvény neve legyen az EHA kódod. A függvény fejléce alá másold be a beadandó feladat címét és szövegét és
a neved. A programban minden fontos részletet (for, if, while blokkok) kommentezz!
Azokban a feladatokban, ahol valamilyen képfeldolgozó műveletet implementálni kell nem használható
a MATLAB Image Processing Toolkit függvény vagy külső fájlt, kódrészlet. Minden munkának egyéni
munkának kell lennie! A Matlab fájlt CooSpace-re kell feltölteni.
0 pontos kötelező feladatok
| Adaptív küszöbölés implementálása | 0 pont |
|
A feladat egy olyan függvény megírása, amely megvalósítja az adaptív küszöbölést téglalap alakú cellákra bontásával. Minden egyes cellákban külön-külön kell meghatározni a küszöbértéket a cellába található intenzitásértékek átlagaként.
|
| Gradiens operátorok implementálása | 0 pont |
|
A feladat a Sobel és a Prewitt gradiens operátorok implementálása. A cél egy szürkeárnyalatos kép gradiens magnitúdó képének előállítása. A függvény paramétereként meg kell adni az input képet és hogy melyik gradiens operátort szeretnénk alkalmazni.
|
| Medián szűrő implementálása | 0 pont |
|
A feladat a medán szűrő megvalósítása. A függvény paramétereként meg kell adni az ablak oldalhosszát pixelben.
|
| Hisztogram széthúzás implementálása | 0 pont |
|
A feladat a hisztogram széthúzás megvalósítása. Feltételezhető, hogy az input szürkeárnyalatos kép intenzitástartománya [0,...,255].
|
| Hisztogram kiegyenlítés implementálása | 0 pont |
|
A feladat a hisztogram kiegyenlítés megvalósítása. Feltételezhető, hogy az input szürkeárnyalatos kép intenzitástartománya [0,...,255].
|
1 pontos kötelező feladatok
| Álszinezés szürkeárnyalatos képen | 1 pont |
|
A feladat egy tetszőleges szürkeárnyalatos képen álszinezés végrehajtása. A szürkeintázitásokhoz RGB értékeket kell rendelni egy meghatározott színskála szerint.
|
| Képrészlet megkeresése a képen | 1 pont |
|
A feladat egy képből kivágott képrészlet megkeresése a képen. Az eredményképen pirossal meg kell jelölni a képrészlet helyét. Előfordulhat, hogy a kódolás miatt nem lesz tökéletes az intenzitás/szín illeszkedés.
|
| A Laplacian of Gaussian (LoG) függvény megvalósítása | 1 pont |
|
A feladat a LoG függvény megvalósítása úgy, hogy a függvény paraméterül kapja a szigma paraméter értékét és az figyelembe vett környezet ablakméretét.
|
| Forgatási transzformáció (forward) megvalósítása szürkeárnyalatos képre | 1 pont |
|
A feladat a forgatási transzformáció megvalósítása szürkeárnyalatos képre. A transzformációnak forward transzformációt kell megvalósítani. Az interpolációs módszert (legközelebbi szomszéd és bilineáris interpoláció) sztring paraméterként kell megadni. A forgatási szög is a függvény paramétere lesz. Az eredmény kép méretét úgy kell meghatározni, hogy az input kép minden részlete látszódjon a képen.
|
| Skálázási transzformáció (forward) megvalósítása szürkeárnyalatos képre | 1 pont |
|
A feladat a skálázási transzformáció megvalósítása szürkeárnyalatos képre. A transzformációnak forward transzformációt kell megvalósítani. Az interpolációs módszert (legközelebbi szomszéd és bilineáris interpoláció) sztring paraméterként kell megadni. A x- és y- irányú skálafaktor is a függvény paramétere lesz. Az eredmény kép méretét úgy kell meghatározni, hogy az input kép minden részlete látszódjon a képen.
|
| Forgatási transzformáció (forward) megvalósítása RGB képre | 1 pont |
|
A feladat a forgatási transzformáció megvalósítása RGB képre. A transzformációnak forward transzformációt kell megvalósítani. Az interpolációs módszert (legközelebbi szomszéd és bilineáris interpoláció) sztring paraméterként kell megadni. A forgatási szög is a függvény paramétere lesz. Az eredmény kép méretét úgy kell meghatározni, hogy az input kép minden részlete látszódjon a képen.
|
| Skálázási transzformáció (forward) megvalósítása RGB képre | 1 pont |
|
A feladat a skálázási transzformáció megvalósítása RGB képre. A transzformációnak forward transzformációt kell megvalósítani. Az interpolációs módszert (legközelebbi szomszéd és bilineáris interpoláció) sztring paraméterként kell megadni. A x- és y- irányú skálafaktor is a függvény paramétere lesz. Az eredmény kép méretét úgy kell meghatározni, hogy az input kép minden részlete látszódjon a képen.
|
| Forgatási transzformáció (backward) megvalósítása szürkeárnyalatos képre | 1 pont |
|
A feladat a forgatási transzformáció megvalósítása szürkeárnyalatos képre. A transzformációnak backward transzformációt kell megvalósítani. Az interpolációs módszert (legközelebbi szomszéd és bilineáris interpoláció) sztring paraméterként kell megadni. A forgatási szög is a függvény paramétere lesz. Az eredmény kép méretét úgy kell meghatározni, hogy az input kép minden részlete látszódjon a képen.
|
| Skálázási transzformáció (backward) megvalósítása szürkeárnyalatos képre | 1 pont |
|
A feladat a skálázási transzformáció megvalósítása szürkeárnyalatos képre. A transzformációnak backward transzformációt kell megvalósítani. Az interpolációs módszert (legközelebbi szomszéd és bilineáris interpoláció) sztring paraméterként kell megadni. A x- és y- irányú skálafaktor is a függvény paramétere lesz. Az eredmény kép méretét úgy kell meghatározni, hogy az input kép minden részlete látszódjon a képen.
|
| Forgatási transzformáció (backward) megvalósítása RGB képre | 1 pont |
|
A feladat a forgatási transzformáció megvalósítása RGB képre. A transzformációnak backward transzformációt kell megvalósítani. Az interpolációs módszert (legközelebbi szomszéd és bilineáris interpoláció) sztring paraméterként kell megadni. A forgatási szög is a függvény paramétere lesz. Az eredmény kép méretét úgy kell meghatározni, hogy az input kép minden részlete látszódjon a képen.
|
| Skálázási transzformáció (backward) megvalósítása RGB képre | 1 pont |
|
A feladat a skálázási transzformáció megvalósítása RGB képre. A transzformációnak backward transzformációt kell megvalósítani. Az interpolációs módszert (legközelebbi szomszéd és bilineáris interpoláció) sztring paraméterként kell megadni. A x- és y- irányú skálafaktor is a függvény paramétere lesz. Az eredmény kép méretét úgy kell meghatározni, hogy az input kép minden részlete látszódjon a képen.
|
| Affin transzformáció (forward) megvalósítása szürkeárnyalatos képre | 1 pont |
|
A feladat affin transzformáció megvalósítása szürkeárnyalatos képre. A transzformációnak forward transzformációt kell megvalósítani. Az interpolációs módszert (legközelebbi szomszéd és bilineáris interpoláció) sztring paraméterként kell megadni. Az affin paraméterek (eltolás, forgatási szög, uniform skálázás) is a függvény paraméterei lesznek. Az eredmény kép méretét úgy kell meghatározni, hogy az input kép minden részlete látszódjon a képen.
|
| Affin transzformáció (backward) megvalósítása RGB képre | 1 pont |
|
A feladat affin transzformáció megvalósítása RGB képre. A transzformációnak backward transzformációt kell megvalósítani. Az interpolációs módszert (legközelebbi szomszéd és bilineáris interpoláció) sztring paraméterként kell megadni. Az affin paraméterek (eltolás, forgatási szög, uniform skálázás) is a függvény paraméterei lesznek. Az eredmény kép méretét úgy kell meghatározni, hogy az input kép minden részlete látszódjon a képen.
|
| Sarokdetektor implementálása | 1 pont |
|
A feladat egy tetszőlegesen választott sarokdetektáló operátor implementálása.
|
| Keresd meg a különbségeket a képen! | 1 pont |
Adott két hasonló kép. Jelöld be piros téglalappal a különbségeket!
forrás: http://upload.wikimedia.org/wikipedia/commons/0/0a/Spot_the_difference.png
|
2 pontos kötelező feladatok
| Niblack algoritmus implementálása | 2 pont |
A Niblack algoritmus egy dinamikus küszöbölő algoritmus. Az algoritmus úgy működik, hogy egy páratlan pixel oldalhosszúságú csúszóablakot kell végigmozgatni a képen. Az ablak közepén lévő pixelre vonatkozó küszöbértéket az ablakban lévő intenzitásértékek átgalágából és szórásból kell meghatározni a
T = μ + k σ
képlet alapján, ahol k valós szám. A Niblack küszöbölést megvalósító függvény parameterei az input kép, a csúszóablak mérete és a k paraméter.
|
| Marr-Hildreth éldetektor megvalósítása | 2 pont |
|
A feladat a Marr-Hildreth éldetektor megvalósítása. A függvény paramétereként kell megadni a két szigma paraméter értékét, valamint az ablakméretet.
|
| Féltónusú (half-tone) kép előállítása szürkeárnyalatos képből | 2 pont |
|
A feladat egy féltónusú kép előállítása szürkeárnyalatos képből: példa
|
| Dithering | 2 pont |
|
Implementálj egy dithering-et megvalósító algoritmust RGB képen.
|
| Kép előállítása mozaikokból | 2 pont |
|
Példa
|
| Fehéredő keret megvalósítása szürkeárnyalatos képre | 2 pont |
|
A feladat fehéredő keret megvalósítása szürkeárnyalatos képre. A keret szélességét (amely nem lehet nagyobb a legkisebb oldalhossz felénél) a függvény paramétereként kell megadni. A fehéredő keret távolságtérkép számításával lehet meghatározni.
|
| Bináris kép címkézésének megvalósítása | 2 pont |
|
A feladat bináris kép címkéző algoritmus (connected-component labeling) megvalósítása. A függvény egy bináris képet és egy számot (4 vagy 8) kap paraméterként. Az utóbbi szám arra vonatkozik, hogy a címkézés során 4- vagy 8-összefüggőséget kell figyelembe venni.
|
3 pontos kötelező feladatok
| Sávok címkézése autópályán | 3 pont |
A feladat egy autpályát/utat ábrázoló szürkeárnyalatos képen a sávok címkézése és megjelenítése különböző színekkel.
forrás: http://ubpost.mongolnews.mn/?p=3313
(A művelet előtt alakítsd szürkeárnyalatossá a képet!)
|
| Hough transzformáció és inverz Hough transzformáció implementálása egyenesekre | 3 pont |
|
A feladat a Hough transzformáció és az inverz Hough transzformáció implementálása egyenesekre.
|
| Hough transzformáció és inverz Hough transzformáció implementálása körökre | 3 pont |
|
A feladat a Hough transzformáció és az inverz Hough transzformáció implementálása körökre.
|
| Morfológiai vázkijelölő algoritmus implementálása | 3 pont |
|
A feladat bináris képből a morfológiai váz kinyerése. A függvény paraméteként kapja az input bináris képet, valamint a szerkesztőelemet (mátrix formában).
|
| Gauss képpiramis előállítása | 3 pont |
|
A feladat egy szürkeárnyalatos kép első 5 szintjének előállítása. A függvény tartalmazza az első 5 képet. Minden képmátrix mérete legyen ugyanakkora és az alacsonyabb felbontásoknál a kép széle legyen feltöltve 0-kkal.
|
4 pontos kötelező feladatok
| Sávok címkézése sávválasztó határolt úton | 4 pont |
A feladat egy szaggatott záróvonallal jelölt úton a sávok címkézése és megjelenítése különböző színekkel.
forrás: http://commons.wikimedia.org/wiki/File:J%C3%B5hvi-Tartu_highway_near_Tartu,_2007-12.jpg
(A művelet előtt alakítsd szürkeárnyalatossá a képet!)
|
| Ablak számlálás épületen | 4 pont |
A feladat egy épület oldalán az ablakok megszámlálása. A számláláshoz címkézés használható.
|
| "Mozgó objektumok" detektálása | 4 pont |
|
A feladat egy állókép-sorozaton meghatározni a "mozgó objektumokat" háttérlevonás segítségével. A "mozgó objektumok" elkülöníthetők a háttértől. Ezeket a képeken a háttérlevonás után címkézéssel kell megjelölni. A végeredmény egy RGB kép, ahol a háttér szürkeárnyalatos, a címkézett objektumok viszont RGB színekkel látható.
|
| Mennyi az idő? | 4 pont |
A feladat a képen látható órán az idő meghatározása. Első lépésként a mutatókat kell szegmentálni, majd meghatározni az időt a mutató állásából.
forrás: http://husvetiajandek.fotopartner.hu
|
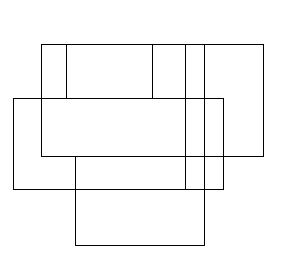
| Hány téglalap látható a képen? | 4 pont |
A feladat a képen látható téglalapokat megszámolni. Segítség: minden téglalapot 1 pixel vékony vonalakkal határozunk meg.
|
| Karakterszámolás nyomtatott lapon | 4 pont |
A feladat egy nyomtatott szöveget tartalmazó szkennelt lapon a karakterek megszámlálása. A függvénynek a karakterek számát kell visszaadnia.
tesztkép
|
