Módszer realisztikus képek előállítására.

Alapelv:

a képen látható felszíni pontok színe (fényessége) más felszíni pontokból kiinduló fénysugarak hatásának az eredménye lehetséges hatások:

 

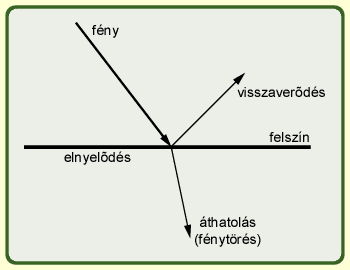
Pl.:	ha csak az egyszeres fényvisszaverődést vesszük figyelembe, akkor csak a direkt megvilágítással kell számolnunk (a más tárgyakról visszavert fényt nem vesszük figyelembe)

nagy számításigény

részei:

látható felszín meghatározása direkt megvilágítás számolása globális megvilágítás számolása árnyék meghatározása ...

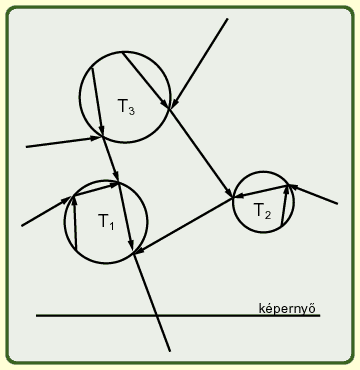
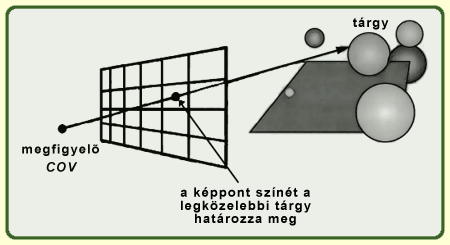
Sugárkövetés (ray tracing) látható felszín meghatározására

követjük a képzeletbeli fénysugár útját a megfigyelőtől a tárgyig

program:

  COV  és az ablak kiválasztása;
  for minden pásztázó vonalra do
    for minden képpontra do
      begin
        fénysugár meghatározása;
        for minden tárgyra do
          if a tárgyat metszi a fénysugár és eddig az
          a legközelebbi metszéspont then jegyezzük meg
          a metszéspontot és a tárgyat;
        a legközelebbi metszésponothoz tartozó tárgy színének 
        megfelelő lesz a képpont
      end;         

utána megvizsgáljuk, hogy a metszéspont a poligon belsejében van-e

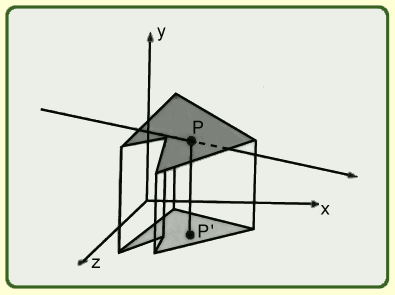
vetítsük párhuzamosan (pl.xz síkra) - elhagyjuk az egyik koordinátát (pl. y), majd megnézzük, hogy P' a vetületben van-e.

tapasztalat:

sugárkövetésnél az idő 75-95%-a a metszéspontok kiszámításával telik el.

gyorsítás:

- konstans kifejezések kiszámítása előre,
- poligonok vetületének kiszámítása előre,
- határoló testek használata,
- tárgyak hierarchikus struktúrákba való rendezése, hogy minél kevesebb metszéspontot számoljunk.

Metszéspontok kiszámítása:

COV:	(x0 ,y0 ,z0)
középpont közepe:	(x1 ,y1 ,z1)
a sugár egyenese:
x = x0 + t(x1 - x0) y = y0 + t(y1 - y0) z = z0 + t(z1 - z0)    = x0 + t·x    = y0 + t·y    = z0 + t·z

metszéspont gömbbel: (a, b, c) középpont,  r sugár:

(x - a)² + (y - b)² + (z - c)² = r²
(x₀ + t·x - a)² + (y₀ + t·y - b)² + (z₀ + t·z - c)² = r²

t-re nézve másodfokú egyenlet,  2,1,0 db megoldás
normális vektor az (x, y, z) metszéspontban:

metszéspont poligonnal:

először meghatározzuk az egyenes és a poligon síkjának  a metszéspontját:

Ax + By + Cz + D = 0

A(x₀ + t·x) + B(y₀ + t·y) + C(z₀ + t·z) + D = 0



(ha A·x + B·y + C·z = 0, akkor az egyenes és a sík párhuzamos),

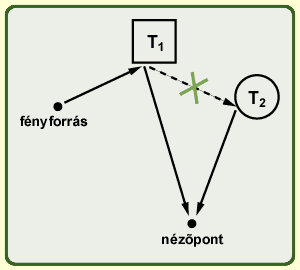
Kövessük a fénysugár útját visszafelé, a nézőponttól kiindulva:

Ha egy fénysugár találkozik egy tárggyal, akkor a tárgy felszínének az a pontja olyan színű lesz, amit a

direkt és globális fénysugarak
az áthatolt fénysugarak

együttesen határoznak meg. Ezeknek a fénysugaraknak a színét úgy határozhatjuk meg, hogy az útjukat visszafelé követjük hasonlóképpen.

a sugarak követése független egymástól
                       
 paralell feldolgozás (transzputer)

 sok geometriai számítás  ( metszéspontok, tartalmazás)

 rekurzió! (követés 3-4 mélységig)