
A mozaikoláshoz hasonló eljárást használunk a megvalósításhoz, ezért hasonló az elnevezése: „dinamikus mozaikolás”, szokták dinamozaikolásnak nevezni.
A HELY – IDŐ TÉR
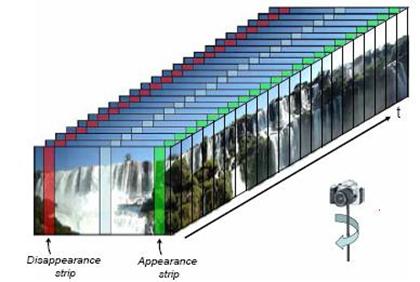
A bemeneti videó képkockáit regisztráljuk (megállapítjuk az egymástól való elmozdulásukat, ezzel tulajdonképpen a kamera elmozdulását is) és elrendezzük őket egy globális tér koordináta rendszerben (u,v). Majd a regisztrált és a tér koordináta rendszerben elhelyezett képkockákat idő szerint is elrendezzük, akkor egy háromdimenziós (u,v,t) koordinátarendszert, az úgynevezett hely – idő teret kapjuk.

1-es ábra forrás
Az ábrán két hely – idő tér reprezentációját láthatjuk, a képkockákat mintha felülről tekintenénk, a kékkel jelzett területek mutatják a mozgókép ezen térben való elhelyezését. Az ábra (a) részén egy álló kamera által rögzített videót, míg a (b) részen egy balról jobbra mozgó kamera által rögzített képsort láthatunk.
A 1-es ábra két felülnézetét mutatja ezen koordinátarendszernek. Ahogyan az ábrán is látszik, statikus kamera esetén (a 1-es ábra (a) része) a hely – idő tér képe egy szabályos téglalap, mozgó kamera esetén (a 1-es ábra (b) része) pedig rombuszról beszélhetünk, ha a kamera állandó sebességgel mozog. Változó sebességgel mozgó videokamera esetén pedig még különösebb, rombuszokból összeállítható alakzatokat figyelhetünk meg. Viszont minden esetben igaz, ha bárhol a t tengelyre merőlegesen veszünk egy metszetet, akkor ez meg fog egyezni az eredeti videó egy képkockájával. A bemeneti videón egy statikus pontot kijelölve, a t tengellyel párhuzamos vonalat kapunk a hely – idő térbeli reprezentációján.
VÁLTOZÓ időszelettel való mozaikolás
A képmozaikolást egy olyan függvénnyel írhatjuk le, amely leképezi a bemeneti képkocka összes pontját az előállított mozaik képre, a képkocka térbeli elhelyezkedése és a pont képkockán belüli helye szerint. Ha csíkokat használunk, akkor az előállítani kívánt mozaik minden egyes oszlopát (sorát) a forrás képkockák oszlopai (sorai) fogják alkotni. Ezen függvényt, folytonos időszeletként reprezentálhatjuk a hely – idő térben.
2-es ábra forrás
ha a videokamera balról jobbra forog, miközben a felvételt készíti, akkor a panoráma dinamozaik első képkockáját a képek jobb végéről – az egyes tárgyak feltűnésének helyéről – kivágott sávokból rakjuk össze (az ábrán zöld színnel jelölt sávok). Majd ezen sávokat a képkockákon ugyanakkora lépésközzel léptetve kapjuk a következő képkockákat (szürke színnel van megjelölve az ábrán). A sávokat egészen a képkockák elejéig – a tárgyak eltűnésének helyéig – léptetjük, ahonnan az utolsó képkockát állítjuk össze (az ábrán a piros sávokkal jelöljük).
Minden időszeletnek az eredeti képekkel vett metszete határozza meg az egyes előállítandó mozaik képekhez szükséges képsávokat. (a .1-es ábrán láthatunk néhány példát ilyen időszeletekre, az ábrán feketével megrajzolt vonalak ábrázolják ezeket) Változó idővonalakat használunk, melyek nem meghatározott alakú felszínek. Ahogy a hely – idő téren végigvonulnak, közben felszínük is szabadon változhat.
panoráma dinamozaikok
Panoráma dinamozaikolásnak nevezzük azon eljárást, amikor a kapott mozgóképből panorámavideót hozunk létre, az eredeti mozgóképen szereplő dinamika megőrzésével. Panoráma dinamozaikolást a fent leírt módszer alkalmazásával is alkothatunk, feltételezzük, hogy a videokamera, ha a 1-es ábra (b) részén látható időszeleteket használjuk a mozaik képek előállításához. Ha balról jobbra forog, miközben a felvételt készíti, akkor az első mozaik képet a bemeneti képkockák jobb széléről vett sávokból állíthatjuk össze, tehát először az egyes területek eredeti videón való feltűnését jelenítjük meg. Ahogyan azt a 2-es ábra is mutatja – ha a videokamera balról jobbra forog a felvétel készítése közben akkor – a bemeneti képkockák jobb oldaláról kezdjük a mozaikolás (zöld sávok). Ez lesz az egyes részek előtűnésének helye – majd ezen sávokkal végigpásztázzuk a hely – idő teret (szürke sávok). Ezekkel az előtűnés és az eltűnés közötti képkockákat hozzuk létre. Végül az egyes részek eltűnését, a mozaikolás befejezését, a bal oldali piros sávok jelképezik az ábrán. Valamennyi ilyen kép a mozgókép képkockáiból panorámaképet alkot. A középső szürke sávok, melyek az egyes régiók feltűnését és az eltűnését kötik össze, a lokális idő szerint haladnak és az egyes régiók dinamikáját teljes mértékben megőrzik. A 3-as ábra egy az előbb leírt technikával készített mozaikot mutat be.

3-as
ábra
a panoráma dinamozaikolás egy másik eredményeképp kapott képkocka
A panoráma dinamozaikokból a felvevő videokamera által rögzített kronologikus idő teljesen eltűnik, ehelyett minden részlet egyszerre tűnik fel, a felvételt készítő videokamera képén való láthatóságát figyelembe véve. Dinamozaikolással sokkal több mindent el lehet érni, mint csak a kronologikus idő figyelmen kívül hagyását. A következő fejezet azt vizsgálja meg, hogy az idővonalak egyes tulajdonságainak változtatásai milyen kihatással vannak az általuk megalkotott dinamozaikokra.
Ezen fejezetben rámutat, hogy a valós idő manipulálás egy speciális esete tulajdonképp az előző fejezetben bemutatott, a panoráma dinamozaikolás módszere – a lokális idő követése, csak egy lehetséges felhasználása a dinamozaikoló technikának. A kronologikus idő formálása nagyon sok olyan (mozgóképekkel dolgozó) alkalmazásnál szükséges lehet, ahol a tárgyak valós idejű megjelenését, láthatóságát esetleg eltűnését valamiképpen át kell alakítani. Az átalakított mozgókép teljesen valósághű marad – köszönhetően annak, hogy a lokális időt mindig megőrzi ezen módszer – még akkor is, ha a tárgyak tényleges feltűnési sorrendjét teljesen megváltoztatjuk.
a videó időben visszafelé történő lejátszása
Ha egy videót visszafelé játszunk le, akkor ebből kézenfekvően következik, hogy a rajta szereplő dinamika is a visszájára fog fordulni. Például egy autó esetében, ha az eredeti mozgóképen balról jobbra elhúz a kamera előtt, akkor a videó visszafelé történő lejátszása esetén ugyanez fordítva történik, ami valósághűségét nem veszíti el, ugyanis az autókkal hátrafelé is szoktak közlekedni. Ami feltűnhet esetleg, hogy a vezető nem hátrafelé néz, miközben az autó hátrafelé mozog. Viszont vannak olyan mozgó dolgok, amelyeket ha rögzít egy videokamera, akkor visszafelé elindítva a kapott mozgóképet – tehát a mozgást megfordítva – a valóságtól teljesen eltérő dolgokat kapunk. Gondoljunk csak egy utcán sétáló emberre vagy akár egy elejtett pohárra, ami a padlón összetörik. Egy vízesés példáján mutatom be, hogy valósághűen is meg lehet fordítani egy videofelvétel lejátszását. A vízesés balról jobbra pásztázása esetén, ha e videóból jobbról balra pásztázást szeretnénk elérni, legegyszerűbb módja, hogy visszafelé játsszuk le a felvételt és elértük a kívánt mozgást. Ez a megoldás igen egyszerű, egyetlen hibája, hogy a videó visszafelé történő lejátszásával elveszítjük annak realisztikusságát, ugyanis az eddig lefelé zúduló víztömeg felfelé kezd csordogálni.
Első pillantásra lehetetlennek tűnik megoldani ezen problémát, hiszen a mozgás szorosan összefügg az idő múlásával és a kamera mozgásával is. Mégis megoldható, a valós idő átformálásával, miközben a mozgóképen lévő dinamikát megőrizzük. Megfigyelhetjük, hogy a panoráma dinamozaikok előállításának módszerénél - ahol minden mozgó tárgy egyidőben végzi a mozgást – semmilyen kikötést illetve szabályt nem tettünk a videokamera mozgásának irányára. Létezik olyan átdolgozási módszer, amely lehetővé teszi, hogy a panorámavideót átalakítsuk egy olyan kameramozgást láttató mozgóképpé, amelynek irányát, illetve sebességét tetszőlegesen megválaszthatjuk.
4-es ábra forrás
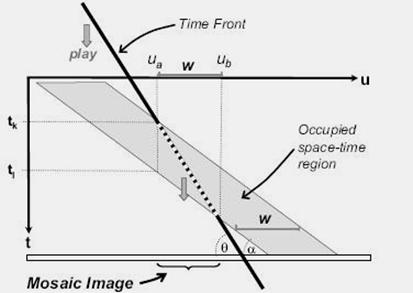
Az ábrán sötétszürke sávval ábrázolt terület jelképezi az input mozgóképet. Ha a videó és a t tengelyre merőleges egyenes által bezárt szögnél (α), - az előbb említett egyenessel – nagyobb szöget bezáró (θ) időszelettel pásztázzuk a hely – idő teret, akkor a mozgókép lejátszásának iránya megfordul. Hiszen az ub pont hamarabb feltűnik a képen, mint az ua – ahogyan ez az ábrán látható – viszont az eredeti videón ua pont megelőzte ub-t. Viszont a mozgóképen látható dinamikát megőrzi, mivel az egyes képrészletek feltűnése és eltűnése között ugyanazon részeken halad az időszelet mint az eredeti videó, ahogyan ez az ua pont esetén is megfigyelhetjük
A 4-es ábrán láthatunk egy olyan egyszerű mozaikalkotási sémát, amely a videokamera mozgási irányát megfordítja, viszont a mozgókép eredeti dinamikáját megtartja. Ezen megvalósítási módszerrel olyan videót készíthetünk, amely a nézőben teljesen valósághű benyomást kelt.
sík idővonallal pásztázás
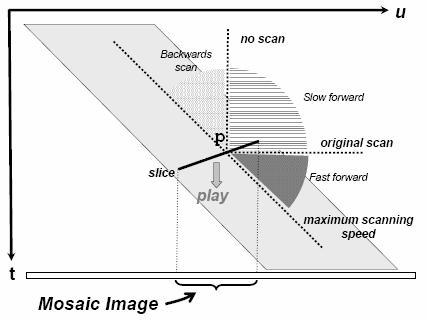
A 5-ös ábrán láthatjuk, hogy milyen különböző esetei lehetségesek a sík időhatárokkal való pásztázásnak. Az időhatárok mindig „lefelé” pásztáznak, hogy megőrizzék az eredeti mozgókép lokális dinamikáját.
5-ös ábra forrás
Az ábrán látható, hogy milyen esetei lehetségesek az idővonalakkal való pásztázásnak, illetve milyen kameramozgás hatását tudunk vele elérni. Az időszelet irányát a P pont körüli forgatással reprezentálhatjuk. Amikor az időszelet dőlésszöge megegyezik az ábrán megjelenített mozgókép dőlésszögével (továbbiakban legyen ez α), akkor beszélhetünk panoráma dinamozaikolásról (a kamera pásztázásának gyorsasága ekkor a legnagyobb). Ha α-nál nagyobb, de az u tengelyre merőlegesnél kisebb szögű időszelettel dolgozunk, akkor a bemeneti videó mozgási irányával ellentétes irányba mozgó mozgókép szekvenciát kapunk. Az u tengelyre merőleges időszelet nem eredményez semmilyen kimenetet. Az u tengelyre merőleges és a t tengelyre merőleges közötti dőlésszögű időszelet esetén lassan előre haladó, míg a t tengelyre merőleges időszelet esetén az eredeti videót eredményezi az eljárás. A t tengelyre merőlegesnél nagyobb dőlésszögű időszelet a videó gyorsabb lejátszását eredményezi (a dőlésszöggel egyenes arányosságban).
A „lefelé”-t itt nem szó szerint kell érteni, sőt előfordulnak olyan esetek is, mikor jobban illene rá a jobbról balra pásztázás, mint például a 4-es ábrán. Itt tk időpontban (ahogy az ábrán épp a θ dőlésszögű időhatár elhelyezkedik) jelenik meg az ua képrészlet és tl időpontban tűnik el (amikor a θ dőlésszögű időhatár jobbról balra pásztázván eléri a mozgókép bal szélét). A fent említett képrészlet a megalkotott dinamozaikból tehát pontosan ugyanúgy tűnik el, mint az eredeti videón. Amely képrészlet hamarabb volt látható, az a végeredményként kapott mozgóképen is hamarabb látható. A különböző időhatárok mind nagyságukban, mind irányukban (akár az u tengellyel bezárt szögüket tekintjük) különböznek egymástól, de ezen két tulajdonságuk nagy mértékben összefügg. A különböző dőlésszögek különböző kameramozgást eredményeznek a készített mozgóképben, alapvetően a kamera mozgásának sebességét határozzák meg, de mint azt a 5-ös ábrán is láthatjuk, a dőlésszög meghatározza, hogy az eredményként kapott videó az eredeti videóhoz képest milyen irányú mozgást végez (az eredetivel megegyező, illetve ellenkező irányban mozog). Ahogyan a 5-ös ábrán is látható, a leggyorsabb pásztázást a panoráma dinamozaikolással érhetjük el, vagyis mikor az időszelet u tengellyel bezárt szöge megegyezik az eredeti mozgókép oldala által kirajzolt határ és az u tengely által bezárt szöggel. Ezen eset viszont magával vonja, hogy a kapott mozgóképünk ekkor lesz a legrövidebb, mivel a kezdeti videóból ekkor látható a legtöbb képrészlet egyszerre. Ebből adódóan a videó látószöge szintén ekkor lesz a legnagyobb. Meg kell jegyezni, hogy a pásztázási sebesség nem összekeverendő a mozgóképen látható dinamika sebességével. Az utóbbit a képkockák sűrítésével, illetve ritkításával befolyásolhatjuk, jelen esetben ez a pásztázás közbeni lépésköz változtatását jelenti.
különleges videóhatások
Az eddig ismertetett módszer kisebb változtatásaival különleges eseményeket tudunk létrehozni speciális esetekben. Ha feltételezzük, hogy a bemeneti mozgókép hely – idő térbeli ábrázolása a 1-es ábra (a) részén látható alakhoz hasonlít, akkor az idővonalak formájának illetve pásztázási sebességének megváltoztatása a legkülönbözőbb hatások elérésére is alkalmassá tesz bennünket. A 6-os ábrán egy stadion robbantásos lebontásáról készült videó, két a fent említett módon megválasztott időszeletet felhasználó dinamozaik képzését láthatjuk. A valóságban a stadion bontása úgy történt, hogy mindenütt egyszerre robbantották fel a robbanószereket. És az épület teljesen egyformán – minden része egyszerre – omlott össze. Ha a 6-os ábra (c) részben látható időszeleteket használjuk egy új videó megalkotásához, akkor egy olyan, valósághű mozgóképet kapunk,

6-os ábra forrás
Egy stadion robbantással való lebontása esetén a (c) illetve (d) részen ábrázolt időszeleteket felhasználva olyan hatást érhetünk el, mintha a robbanószereket nem egyszerre robbantották volna fel, hanem (a) esetben először a stadion szélén, majd a közepén, (b) esetben pedig épp fordítva, azaz először a stadion közepén és végül a szélén robbantottak volna
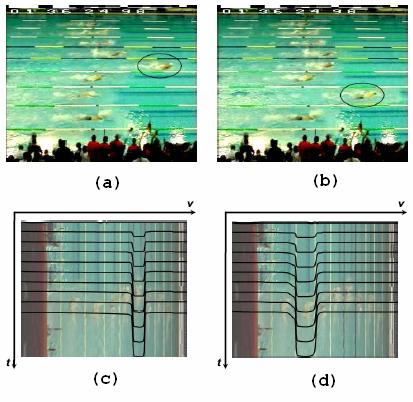
amelyen a stadion oldalai kezdenek leomlani először, és a középső része csak a legvégén omlik össze. Ezzel szemben, ha az ábra (d) részén felrajzolt időszeleteket használjuk, akkor éppen ellenkező hatást érünk el, vagyis a stadion közepe omlik először össze, és az oldalai csak a végén kerülnek sorra. Az (a) és (b) részen a kezdeti képkockák egyikét láthatjuk, a különbség a két videó között ezeken is igen szembetűnő. Egy másik példa egy úszóverseny, ahol tulajdonképpen mi választhatjuk meg, hogy ki legyen a verseny győztese. Itt is, mint az előző esetben, álló kamerával rögzítjük a mozgóképet. Ezen esetben viszont a videót 90 fokkal elforgatva ábrázoljuk a hely – idő térben (az ábrán meg is figyelhető,
7-es ábra forrás
Az úszóverseny győztesét is megválaszthatjuk a dinamozaikolás segítségével. A (c) részen megadott időszeletek segítségével az 5-ös pályán versenyző úszót, amíg az ábra (d) részén megadott időszeletekkel a 7-es sávban versenyző úszót tudjuk győzelemhez juttatni.
hogy a v tengelyt ábrázoltuk nem pedig az u-t). Az egyes medencesávokat figyelembe vesszük és a 7-es ábra (c) és (d) részén láthatóhoz hasonló megfelelő időhatárt alkalmazunk, akkor ezzel a kívánt úszót segíthetjük a győzelemhez. Ebben az esetben kihasználtuk, hogy az úszók párhuzamos vonalakkal vannak elválasztva, ám a fenti hatások eléréséhez ez nem szükséges. Tulajdonképpen egyedüli feltételként az szabható meg, hogy az egyes mozgó tárgyak ne keresztezzék egymás mozgását, ekkor ugyanis különböző anomáliák, mint például a tárgyak többszöri feltűnése fordulhat elő.
egymást erősítő időhatárok
Egyszerűség kedvéért tekintsük csak a két dimenziós esetet, amikor a mozgás csak az u – t tengely mentén látható. Torzítást azon mozgások jelentenek, amelyek a kamera mozgási irányával párhuzamosan végeznek elmozdulást a képen. A kamera mozgási irányára merőleges elmozdulások csak alig észrevehető torzítást okoznak. Tekintsük a hely – idő tér azon részét, ahol az időszeletek és a mozgó tárgyak kölcsönhatásba kerülnek. Ha αs – el jelöljük a t tengely és az adott részen érvényes időszelet közötti szöget, akkor αs = π/2 esetén semmilyen torzítás nincs, hiszen ekkor a képkockákat az eredeti videó képkockái alkotják. α0 – al jelöljük az idő (t) tengely és a mozgó tárgy útja közötti szöget. Ha α0 = 0, úgyszintén nem tapasztalunk torzítást, hiszen ekkor a tárgy mozdulatlan. A további esetekben a tárgyak szélessége csökkenni illetve nőni fog a fenti szögek függvényében. Az eredeti és a végeredményként kapott szélesség arányát a következő képlettel tudjuk leírni:
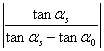
Dinamozaikok esetében a torzítás egy virtuális „lyuk” - kamera pásztázásaként írható le, ha a hely – idő teret egyenes időszeletekkel alakítjuk át. Az általános esethez hasonlóan a tárgyak új szélessége (wúj – jal jelölve) a következő egyenlettel határozható meg:
![]()
ahol vp a pásztázó lyukkamera, míg vt a mozgó tárgy sebessége. A kamera pásztázásával ellenkező irányban mozgó tárgyak negatív sebességgel rendelkeznek (vt < 0), vagyis ahogy a képletből is látszik a fenti hányados kisebb lesz mint egy, azaz a tárgy szélessége csökkenni, a kamera mozgásával megegyező irányban mozgást végző tárgyak szélessége pedig nőni fog. A képletről szintén leolvasható, hogy igen nagy vp esetén – vagyis ha a kamerapásztázás sebessége a tárgy sebességéhez képest igen nagy – akkor a tárgy szélessége elhanyagolhatóan változik csak meg ( wúj ≈ weredeti ).
A jól ismert Doppler effektust – amikor egy jel magasabb frekvenciái nagyobbá, alacsonyabb frekvenciái pedig még kisebbé válnak -a fent leírt szélesség növekedés és csökkenés következtében itt is megfigyelhetjük.
tördelt időszeletek
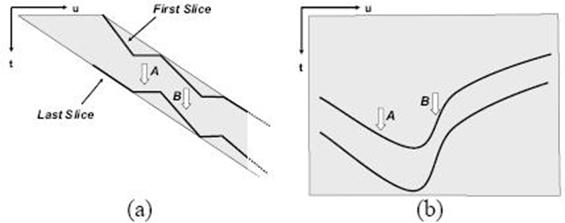
Az időszeletek dőlésszögének változtatásával lehetőségünk van a torzítás egyes régiókban való csökkentésére (ahol számunkra fontos tárgyak mozognak), ennek viszont velejárója, hogy más részeken növeljük a torzítás valószínűségét. Ahogyan azt a 8-as ábra is mutatja, ahol a torzítást csökkentenünk kell, ott kisebb dőlésszögű időszeletet (az ábra (a) részén az A-val jelölt időszelet), ezzel szemben, ahol a torzítás elhanyagolható – például állandó részeken, ahol a képen nincs semmilyen mozgás – az
8-as ábra forrás
Tördelt időszeletek. Az ábra (a) részén a diszkrét esetet láthatjuk, amikor az időszeletet több egyenes szakaszból rakjuk össze. A (b) részen a folytonos eset látszik, amikor az időszeletek görbék segítségével adottak. Ezen időszeletekkel lehetőségünk nyílik a torzítás kiküszöbölésére, csökkentésére.
időhatárokat nagyobb dőlésszögűeknek is vehetjük (az ábra (a) részének B-vel jelölt idő szelete). Ha szeretnénk valósághű mozgóképet alkotni, akkor figyelnünk kell arra is, hogy a különböző dőlésszögű időszeletek különböző szélességű tárgyakat alkothatnak a képen, így a dőlésszög megváltoztatásakor a környezet torzításán kívül ezt is figyelembe kell vennünk. Az időszeletek dőlésszögének beállítása részben a felhasználótól függő feladat, hiszen szubjektív vélemény alapján dönti el mindenki, hogy az adott mozgókép mely része fontosabb számára, hol enged meg kisebb torzításokat, és hol szeretne teljesen torzításmentes képeket. Ennek ellenére néhány dologban a számítógép segítheti ezen kiválasztást.
Próbálkozhatunk megadni költség - célfüggvényeket, majd ezek minimalizálásával megtalálni az optimális megoldást. Ezen megoldás hátránya, hogy nem garantálható olyan célfüggvény létezése, amely a kívánt eredményt adná, hiszen az ember szubjektív véleményére van bízva, hogy milyen végeredményt szeretne elérni. Sőt olyan tényezőket is figyelembe kell vennünk, hogy az emberi látás sokkal érzékenyebb a homogén, szilárd testeken látható zajra, torzításokra, mint a textúrált területeken feltűnő különböző hibákra.
A legkézenfekvőbb és legegyszerűbb megoldás, ha teljes mértékben a felhasználóra bízzuk az időszeletek megadását. Ekkor viszont nagyon pontos felhasználói felületre van szükség, amelyről a kijelölt időszeleteket le tudjuk olvasni. A felhasználótól pedig e probléma alapos ismeretét és az időszeletek gondos megadását várjuk el. Egy másik megoldás lehet a mozgó tárgyak követése. Ekkor a kimeneti mozgókép azon képkockáit, melyeken a mozgó tárgy megjelenik, csak egy bemeneti képkocka vagy néhány egymást követő képkocka segítségével alkotjuk meg. Ezen eljárás igen időigényes és nagyon bonyolult is lehet, például egy csapat ember mozgásának követése esetén nagyon sok átfedés, nagyon összetett mozgások fordulhatnak elő. De akár a háttérbe beleolvadó mozgó tárgyakat is említhetnénk, amelyek esetén már a mozgó tárgyak követése sem egyszerű.
A 9-es ábrán láthatunk a torzításra egy példát. Itt a torzítást maga az a cselekvés okozza,

9-es ábra forrás
az utcai előadó gyors, szinte egy helyben való mozgása az általános időszeletekkel torz képet alkot. A 9 - es ábra (a) részén látható időszeletekkel a jobb oldali, tiszta képet tudjuk megalkotni.
hogy az utcai előadó gyorsan és viszonylag sokat mozog előre és hátra kis területen. Ha alaposan megfigyeljük, akkor a torz képen is láthatjuk, hogy az illesztés tökéletes (a ház minden egyes íve megfelel a valóságnak), egyedül az előadó torzult a képen el. A jobb oldali képet a 9-es ábra (a) részén látható időhatárokkal készítették. Ezen példa is mutatja, hogy milyen hatékony lehet a tördelt időhatárokkal való pásztázás a hely – idő térben.