• Introduction
• Project
• Solutions
• The Team
• Download

Solutions

The Duuh Algorithm

The main idea is to find first possible pixel from two projections (horizontal and vertical) and put it on the result image; then re-iterate the process until there is no more possible ways to put a pixel on the result image.

This method uses only two projections, making it very fast, but it has a lot of errors, like it is shown in the results.

Comparing with the previous method (evolutionary algorithm), this method doesn’t take a priori information, like the shape of the objects in the image.

This method could be slightly improved by using multiple projections, but one should not expect great results.

Star section algorithm

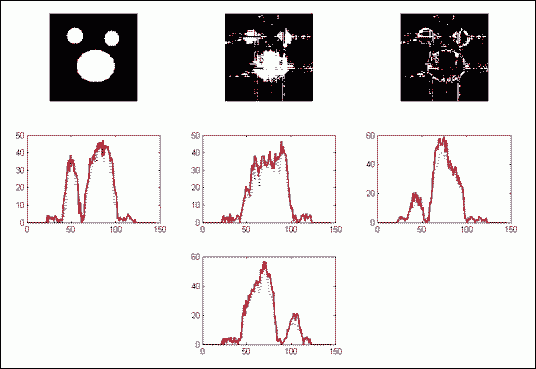
This algorithm uses multiple projections of the image and tries to find the maximums of each projection and obtain a point of image. Next it starts with this pixel going in different directions, checking if there could be other object pixels, until there couldn’t be more object pixels. Next will re-iterate by finding the maximums of the projections again, choosing a new object pixel, and so on. The algorithm stops if there are no changes between two iterations.

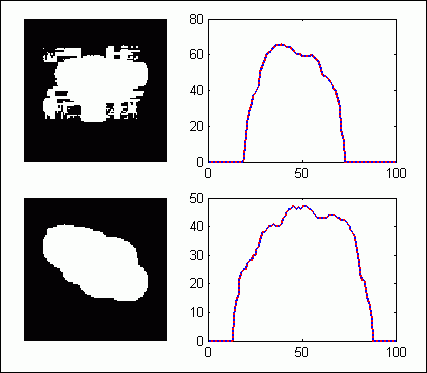
Following there are presented the results of using this algorithm, in the upper left image is the original object, in the lower left image is the reconstructed object, in the upper and lower right parts the projections are presented, in red the original projections and in blue the resulting projections.

2 projections results

4 projections results

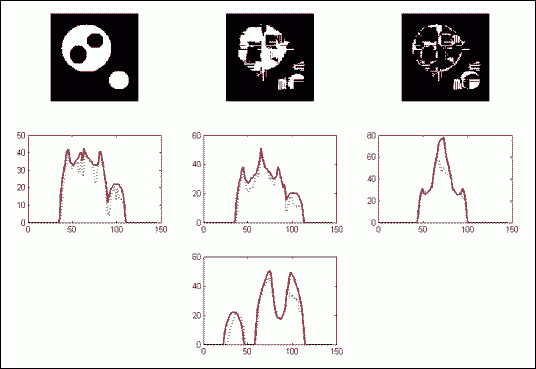
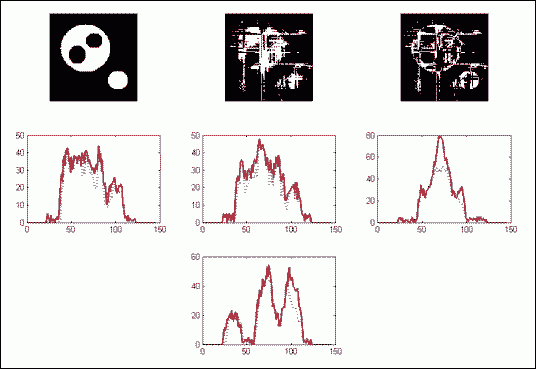
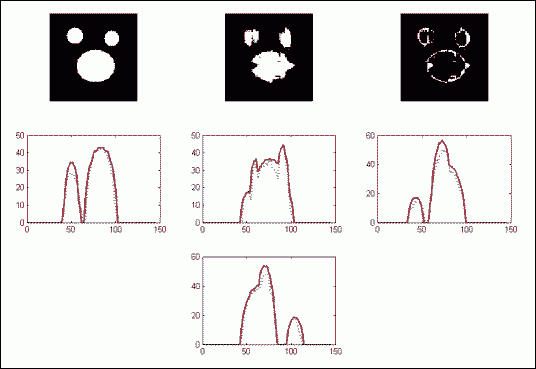
Next are presented the results for using four projections of the image at 0, 45, 90, 135 degrees. In the left part are presented the reconstruction results for the case of no noise and in the right part are presented the results when having 5% noise.

Evolutionary Algorithm for 2D objects

The initial population is randomly generated, growing this population using two operators: mutation and crossover. We have used 1000 instances for the initial population.

The mutation operator has only one parent (source instance) and it generates one offspring, the difference between the parent and the offspring could be the number of disks or the size or the coordinates of one randomly chosen disk.

The crossover operator mixes the features (coordinates) from the two parents and generates two offspring.

For these operations we have imposed a constraint that is the resulting offspring must have only disjoint disks.

The "fitness" of an instance is measured by the error (difference) between its projections and the desired projection. Based on the fitness of instances we select only the most 1000 fittest ones for the following generation (iteration).

Results

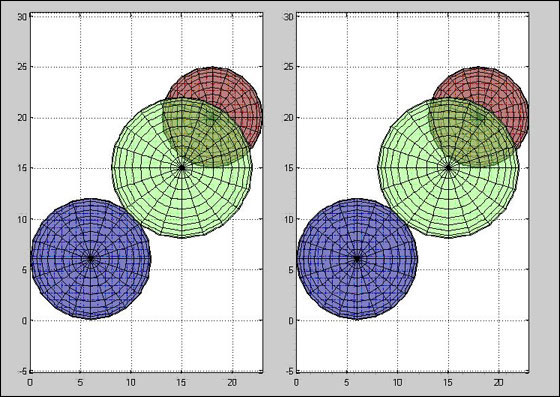
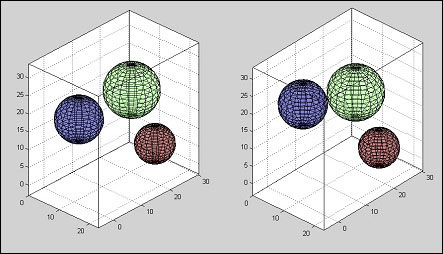
Evolutionary Algorithm for 3D objects

The algorithm is the same that the one in 2D case, but there is no outer ring and the objects (that are spheres now) can overlap and also partially can get out of the image boundaries.

For 3D reconstruction we have used three projections for each Cartesian plane.

Modified randomized Kaczmarz algorithm

Kaczmarz algorithm is an iterative method for solving linear equation systems, like the one in our problem.

It has been observed in the numerical simulations that the convergence rate of Kaczmarz method can be significantly improved when the algorithm sweeps through the rows of A in a random manner, rather than sequentially in the given order. In fact, the improvement in convergence can be quite dramatic. We are using a specific version of this randomized Kaczmarz method, which chooses each row of A with probability proportional to its relevance - more precisely, proportional to the square of its Euclidean norm.

Random Kaczmarz Algorithm: Let Ax=b be a linear system of equations and let be arbitrary initial approximation to the solution.
For k=0,1,... compute:

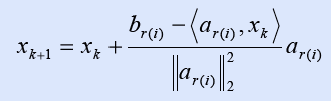
where r(i) is chosen from the set {1,2,...,m} at random, with probability proportional to

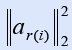
This method is usually used in discrete tomography. Although with some modifications it could be used in binary tomography.

This algorithm was modified for preventing a pixel’s value to exceed the limits ([0,1]), but in the same time to preserve the increment energy.

Following three results of this method are presented. For obtaining these images 500 iterations were done and were used 20 projection planes.

From these images it can be seen that the results compared to other methods are worse. This can be explained by the fact that this method is usually used for discrete images. For getting a better result in binary images it is needed to be found a better heuristic solution for redistributing incremental energy which is added in every iteration step to a pixel's value.