Fast Fourier transzformáció
Hol volt, hol nem volt, létezett egy Fourier transzformáció, amit az egyetem számos kurzusán megkíséreltek megtanítani nekem, de én mégsem értettem meg. Felbuzdulva azon, hogy a kedvenc előadóm egy két órás előadást tartott erről az egészen *magic* számba ment dologról, úgy gondoltam, hosszú wikipedia és tankönyv olvasgatás helyett, amiben több a képlet és a matek, mint amit képes egy infós szem felparsolni, végignéztem az előadást. És megtörtént a csoda! Hát ez egy hihetetlenül egyszerű cucc! A továbbiakban a Fourier transzformáció mögötti varázslatot tárom fel.
Kedves olvasó, készüj rá fel, hogy egy nagyon hosszú posztot fogsz olvasni ![]()
A problémafelvetés:
Polinomokkal szeretnénk műveleteket végezni. A komplex számok teste feletti egyváltozós polinomok olyan $$A(x)=a_0+a_1x+\dots+a_{n-1}x^{n-1}$$ alakú kifejezések, ahol $n \ge 0, n \in \mathbb{Z}$ szám (tehát nemnegatív egész), valamint $a_0,\dots,a_{n-1} \in \mathbb{C}$.
Szokás őket rövidebb formában is reprezentálni, például:
- összegként: $\mathop{\sum}\limits_{k=0}^{n-1}a_kx^k$
- vektorként: $<a_0,a_1,a_2,\ldots,a_{n-1}>$
Műveletek polinomokon:
Kiértékelés:
Adott $A(x)$ és egy $x_0$ szám. Keressük: $A(x_0)$ értéket.
Ennek megoldására például Közelítő és szimbolikus számításokból (továbbiakban köszi) tanuljuk a Horner elrendezést:
\[p(x)=a_0+x(a_1+x(a_2+\ldots x(a_{n-1})\ldots))\]
Így $O(n)$ idő alatt ki lehet számolni a helyettesítési értéket. (Ahol $n$ az aritmetikai műveletek száma, pl $2$ szám összeszorzása is ilyen. Itt pedig $n$ szorzást és $n$ összeadást kell csinálni.)
Összeadás:
Adott az az $A(x)$ és $B(x)$ polinomok. Keressük a $C(x)=A(x)+B(x)$ polinomot.
Ezt is könnyen ki tudjuk számolni: $A(x)=a_0+a_1x+\dots+a_{n-1}x^{n-1}$ és $B(x)=b_0+b_1x+\dots+b_{n-1}x^{n-1}$.
Ekkor $c_k=a_k+b_k$ minden $k$-ra. (Ha nem egyforma a fokszám, azokat az elemeket $0$-nak vesszük.)
Ez is $O(n)$ időben kiszámítható.
Szorzás:
Adottak az $A(x)$ és $B(x)$ polinomok. Keressük a $C(x)=A(x)\cdot B(x)$ polinomot.
Ebben az esetben az $A(x)=a_0+a_1x+\dots+a_{n-1}x^{n-1}$ és $B(x)=b_0+b_1x+\dots+b_{n-1}x^{n-1}$. polinomokból összehozni a következőt:
$$C(x)= a_0b_0+(a_0b_1+a_1b_0)x+\ldots$$
Azaz minden $c_k=\mathop{\sum}\limits_{j=0}^{k}a_{j}b_{k-j}$ (a $j$-edik és a $k-j$-edik tagok együtthatóinak szorzatának összegéből kapjuk a $k$-adik fokú tag együtthatóját.)
Ez így $O(n^2)$ idő, ami sok! Ezt szeretnénk kiszámolni $O(n \log n)$ időben.
Miért is fontos, hogy a polinomszorzást gyorsan tudjuk kiszámolni? Mert igazából megegyezik egy gyakorlatban sokszor alkalmazott művelettel, amit konvolúciónak nevezünk.
Konvolúció:
A konvolúció "vektorok" belső (skalár) szorzata minden lehetséges eltolásra. Nézzünk egy példát: van egy sűrűn hullámzó függvényünk (pl valami zajjal terhelt jelünk), amit szeretnénk "kisimítani". Ezt megtehetjük úgy, hogy egy Gauss-függvényt a saját függvényünk minden egyes pontjára ráillesztünk és az adott pont új értékét a két függvény szorzata adja. Valahogy úgy, mint a következő képen (ahol a sok színes sombrero alakú függvényt hívjuk Laplacian of Gauss-függvénynek):
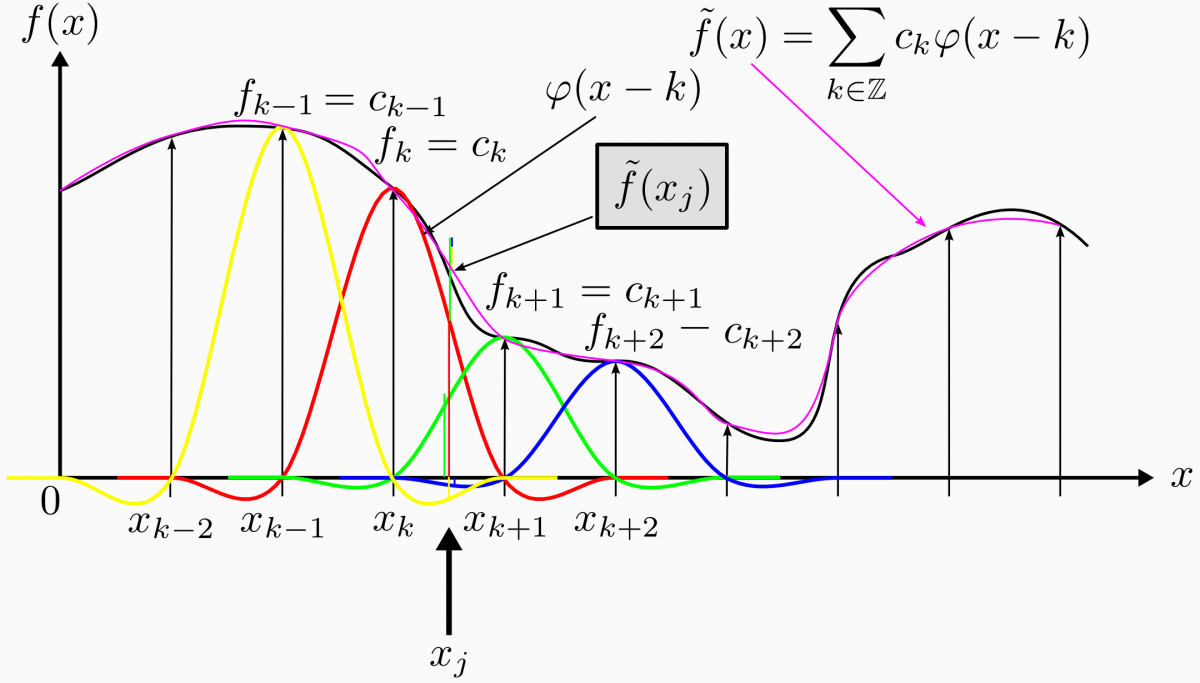
Tehát a Gauss-függvény jelen esetben azt fogja megmondani, hogy az adott pont mekkora környezete mennyire számít az új érték kiszámolásakor. Van  erre egy real time videó is itt: https://www.youtube.com/watch?v=D0F-NPerCIE. Konvolúciót alkalmaznak még például a képfeldolgozásban is zaj szűrésre, simításra, éldetektálásra. Ahol szintén a kép minden pontjára kell kiszámolni két függvény (ami itt épp két mátrixként van reprezentálva) konvolúcióját.
erre egy real time videó is itt: https://www.youtube.com/watch?v=D0F-NPerCIE. Konvolúciót alkalmaznak még például a képfeldolgozásban is zaj szűrésre, simításra, éldetektálásra. Ahol szintén a kép minden pontjára kell kiszámolni két függvény (ami itt épp két mátrixként van reprezentálva) konvolúcióját.
A konvolúció képlete általánosan egy dimenzióban a következő:
$$c_k=\sum_{j=-\infty}^{\infty}a_jb_{k-j}$$
Ekkor $b$ mondja meg, hogy egy pont környezete milyen súllyal számít és $k$ az eltolás (hogy éppen hanyadik pontot számítjuk ki).
A szemfülesek már észrevehették, hogy ez a képlet olyan, mint a polinomszorzás végtelenre kiterjesztve. Egyrészt ez azért van, mert előfordulhat, hogy nem tudjuk, hogy a függvényünk milyen hosszú lesz (pl egy jelsorozat esetében), másrészt mert ha a súlyfüggvény valami véges méretű - ahogy a Gauss is - , akkor úgy tekintünk a rá, mintha sok különálló függvényből lenne "összerakva". Az egy dimenziós konvolúció egyszerűen kiterjeszthető további dimenziókra, de ebben a posztban csak az egy dimenziós esetre lesz szükségünk.
A wikipédián van is egy szemléletes animáció: https://upload.wikimedia.org/wikipedia/hu/0/0a/Convanim_expminus_gauss_hu.gif
Hogyan tovább?
Azt már láttuk, hogy ezt a műveletet vektoros reprezentációban nem lehet hatékonyan megvalósítani. Beszéljünk egy kicsit a többi reprezentációról is!
Gyökök
Egy polinomot a gyökeivel $r_0, r_1,\ldots,r_{n-1}\in\mathbb{C}$ reprezentáluk - és minden polinomot be tudunk azonosítani a gyökeivel. Egy $n$-edfokú polinomnak $n$ gyöke van. Ekkor a polinom: $A(x)=c(x-r_0)(x-r_1)\ldots(x-r_{n-1})$.
Műveletek:
- Kiértékelés: easy. Az $x$-ek helyére behelyettesítünk, és végrehajtjuk a szorzásokat.
- Szorzás: egymás után írjuk + összeszorozzuk a főegyütthatókat
- Összeadás: csupán a gyökökkel összeadást nem tudunk támogatni, szóval vissza kell transzformálni együttható vektoros alakba ($O(2^n)$), majd összeadjuk ($O(n)$), majd vissza kéne transzformálni ebbe az alakba. Erre a visszatranszformálásra egyáltalán nincs módszerünk!
Alappontok
A polinomot $(x_0,y_0), \ldots , (x_n,y_n)$ párokkal adjuk meg, ahol $A(x_i)=y_i$ minden $i$-re (minden $x_i$ páronként különböző). Nézzük meg a műveleteket rajtuk egyesével:
Kiértékelés:
Kösziből tanuljuk a Lagrange interpolációt, amely $n+1$ alappontra egy $n$-edfokú polinomot illeszt és ez $O(n^2)$ időben kiszámítható. Szóval a kiértékelés úgy megy, hogy megalkotjuk a polinomot Lagrange interpolációval, majd azt kiértékeljük az adott helyen (mondjuk egy Horner elrendezéssel). Tehát egy egyszerű dologra van egy rém bonyolult megoldásunk.

Összeadás:
Ha az alappontok ugyanazok és ugyanannyian vannak: csak egyenként összeadjuk az $y_i$-ket ($O(n)$ lesz, ezt szeretjük!)
Ha nem: Gyártani kell plusz kiértékeléseket a különböző alappontokhoz és utána összeadni
Szorzás:
Egyenként összeszorozzuk az $y_i$-ket.
Majd legyártunk még lineáris sok új alappontot. (Pl két $10$-edfokú polinom -- $11$ alapponttal -- szorzata $20$-adfokú, amihez $21$ alappont kell.)
Ha mégis elég sok alappontunk van, akkor egyszerűen összeszorozzuk az $y_i$-ket. (Ebben az esetben ez gyors.)
Szóval kapjuk a következő táblázatot a lehetséges reprezentációkban elérhető futásidőkről, ami nem túl biztató: nincs igazán jó reprezentációnk.
| Vektoros | Gyökök | Alappontok | |
|---|---|---|---|
| Kiértékelés | $O(n)$ | $O(n)$ | $O(n^2)$ |
| Összeadás | $O(n)$ | $\infty$ | $O(n)$* |
| Szorzás | $O(n^2)$ | $O(n)$ |
$O(n)$* |
*Abban az esetben, ha szorzás esetén elég sok alappontunk van, összeadás esetén pedig ugyanannyi és ugyanazok az alappontok.
Tehát nem tudunk egy reprezentációban mindhárom műveletre hatékony algoritmust mondani. Mi lenne, ha ami az egyikben rossz, azt a másikban csinálnánk meg? Lehet-e elég gyorsan áttranszformálni egyikből a másikba? A gyökös reprezentáció nem lesz használható, mert vektoros formába nem tudunk visszatranszformálni belőle. Tehát a vektoros és alappontos reprezentáció közötti váltást kellene gyorsan (kevesebb, mint $O(n^2)$ idő alatt) megcsinálni. Hiszen másképp nem érné meg a transzformációt elvégezni. A vektoros reprezentáció esetén a szorzás lassú. Ezt kellene áttranszformálni alappontos formába úgy, hogy elég sok alappontot gyártsunk ahhoz, hogy ott a szorzás elvégzése $O(n)$ idő alatt kiszámítható legyen. Az ezt megvalósító transzformáció a Fourier transzformáció. Oda-vissza $O(n\log n)$ idő alatt tudunk a segítségével transzformálni.
Oszd meg és uralkodj algoritmus
Cél: Ha adott egy $A(x)$ (együtthatóvektoros alakban) polinom és alappontoknak egy $X$ halmaza, kiszámolhatjuk minden $x\in X$-re a polinom helyettesítési értékét gyorsan.
Oszd meg:
Osszuk fel az $A$ együtthatóvektorát két különböző vektorra:
$A_{even}(x) =\mathop{\sum}\limits_{k=0}^{(n-1)/2} a_{2k}x^k$ és $A_{odd}(x) =\mathop{\sum}\limits_{k=0}^{(n-2)/2} a_{2k+1}x^k$
Azaz kapunk egy $<a_0,a_2,a_4, \ldots>$ és egy $<a_1,a_3,a_5,\ldots>$ vektort
Uralkodj:
Csináljunk alappontokat rekurzívan: $A_{even}(y)$ és $A_{odd}(y)$ kiértékelése $y\in\{x^2|x\in X\}$
Kombináld:
$$A(x)=A_{even}(x^2)+x A_{odd}(x^2)$$
Megjegyzés: vegyük észre, hogy a képletben csak $x^k$ szerepel. Ha ennek helyére $x^2$-et helyettesítek kapom, hogy $x^{2^{k}} = x^{2k}$. Ekkor a párosak esetében stimmel is, amit kapunk, az $a_{2k}$ együtthatót az $x^{2k}$-val szorozzuk össze. A páratlanhoz azért kell az $x$-szel való szorzás, hogy az $a_{2k+1}.$ együtthatót ne az $x^{2k}$-val szorozzuk össze.
Ennek a listának a kiszámítása lineáris időben megy.
Időigény: Ezzel csak a polinom mérete csökken. Az algoritmus így $O(n^2)$ időigényű. Csökkenteni kellene az $X$ méretét is. Ahhoz, hogy az $O(n\log n)$-es időt el tudjuk érni, minden rekurzív híváskor a felére kell csökkentenünk az $X$ méretét.
Nézzük mekkora lehet $X$ mérete:
- $|X|=1$ $X=\{1\}$
Ha $X$ egy elemű, akkor választhatjuk mondjuk az $1$-et alappontnak - $|X|=2$ $X=\{-1,1\}$
Az $1$ négyzetgyöke a $-1$ és az $1$ - $|X|=4$ $X=\{-i,i,-1,1\}$
Az $1$ négyzete a fentiek szerint a $-1,1$-nek, a $-1$ pedig négyzete a $-i,i$-nek is - $|X|=8$ $X=\{\pm \frac{\sqrt{2}}{2}(1+i),\pm \frac{\sqrt{2}}{2}(1-i),-i,i,-1,1\}$
Tehát ilyenkor $X^2$ mérete a fele lesz az $X$ méretének (amikor lentről haladunk a felsorolásunkban felfelé). Ez jó, mert négyzetre emeléskor csökken az alappontok száma és pont ezt akarjuk elérni.
És a $8$ méretű $X$-ben lévő elemeket sem Dumbledore varázsolta oda, hiszen ezeket az értékek ismertek. (Ha hamarabb nem, Diszkrét matematika órákról biztosan.) Ezek bizony az egységgyökök. Olyan értékek, amik egy egységkörön - 1 sugarú kör - helyezkednek el.

$n.$ egységgyökök:
Az $n.$ egységgyökök azok a komplex számok, melyek $n.$ hatványa $1$. Általában a következő alakban adjuk meg őket:
$$\cos\Theta+i\sin\Theta$$
$\Theta=0,\frac{2\pi}{n},\frac{4\pi}{n},\ldots,\frac{2(n-1)\pi}{n}$
Ezt felírhatjuk Euler alakkal is:
$$\cos\Theta+i\sin\Theta = e^{i\Theta}$$
A trükk: Négyzetre emeléskor ${e^{i\Theta}}^{2}=e^{i2\Theta}\mod 2\pi$, azaz amikor egy egységgyököt négyzetre emelünk csak a szögét duplázzuk meg a valós tengelyhez képest, tehát ugyanúgy egységgyököt fogunk kapni.
Ha $|X|=2^k$, akkor az $n.$ egységgyököket alappontnak választva az $|X^2|=2^{k-1}$ lesz. Ezért az előbbi ,,Oszd meg és uralkodj'' algoritmus $O(n\log n)$ időigényű. Ezt hívjuk Fast Fourier transzformációnak.
Polinomszorzás gyorsan
- $A^*=FFT(A)$
- $B^*=FFT(B)$ Ekkor az alappontok megegyeznek, ha mindkét polinom fokszámát egyformára hoztuk, de ez vektortérben könnyű!
- $C^*_k=A^*_k\cdot B^*_k$
- $C=IFFT(C^*)$
Ha kíváncsi vagy, hogy ez formálisan miért működik és hogyan kell az inverz transzformációt megcsinálni, a videóban megtalálod:
