A probléma a következő: Adott $k$ db rendezett lista $(L_1, L_2, \ldots, L_k)$, mindegyik hossza $n$ és mindben meg akarjuk talalni az $x$-et vagy ha nincs benne, annak rákövetkezőjét.

Erre a triviális, ám kevésbé hatékony megoldás, hogy indítunk $k$ független bináris keresést. Ezt megtehetjük, hiszen a bináris keresés használatának feltétele az, hogy a listánk rendezett legyen. Ezzel a módszerrel $O(k\log n)$ időt használunk fel, hiszen egy bináris keresés $O(\log n)$ ideig tart és ezt $k$ db listában kell végrehajtsuk.

A cél ezt a problémát $O(k+ \log n)$ időben megoldani. Ehhez fogjuk felhasználni a fractional cascading módszert. A módszer lényege, hogy miután az első tömbben megtaláljuk a keresett elemet, ennek helyét a többi listában való kereséshez is újra felhasználjuk valahogyan. Ehhez viszont néhány plusz információt kell a listáinkhoz hozzáadni.

Először is definiáljunk új listákat, legyenek ezek $L'_1,\ldots,L'_k$ úgy, hogy $L'_k=L_k$ - a legalsó listát nem bántjuk - és minden $i<k$-ra legyen $L'_i$ az $L_i$ és $L'_{i+1}$ beli minden második elem összeolvasztásának eredménye. Jegyezzük meg, hogy $|L'_i|=|L_i|+1/2 |L'_{i+1}|$, tehát $|L_i|\leq 2n=O(n)$, tehát tárban is jók vagyunk. A "legfelső" tömb sem lesz túl nagy, hiszen a $k.$ lista tárigénye az $S(k)=n+S(k-1)/2$ rekurzív összefüggés alapján számolható, azaz az eredeti $n$ elem a $k.$ listában, és ehhez jön még az alatta lévő lista elemszámának fele. Ez pedig egy geometriai sor: $n+n/2+n/4+n/8+\ldots = 2n$. Ami azt jelenti, hogy a legnagyobb lista kétszer akkora lesz, mint az input listák eredeti mérete. Ez azért is jó, mert egy ekkora listában az eredeti mérethez képest csupán eggyel több lépést kell végrehajtanunk, ha bináris keresést alkalmazunk.

Nézzünk erre egy példát! Az eredeti listáink a következők:

$L_1=\{4,6,8,12,20\}$

$L_2=\{1,2,11,15,27\}$

$L_3=\{0, 5, 7, 9, 17\}$

$L_4=\{1, 8, 10, 21, 30\}$

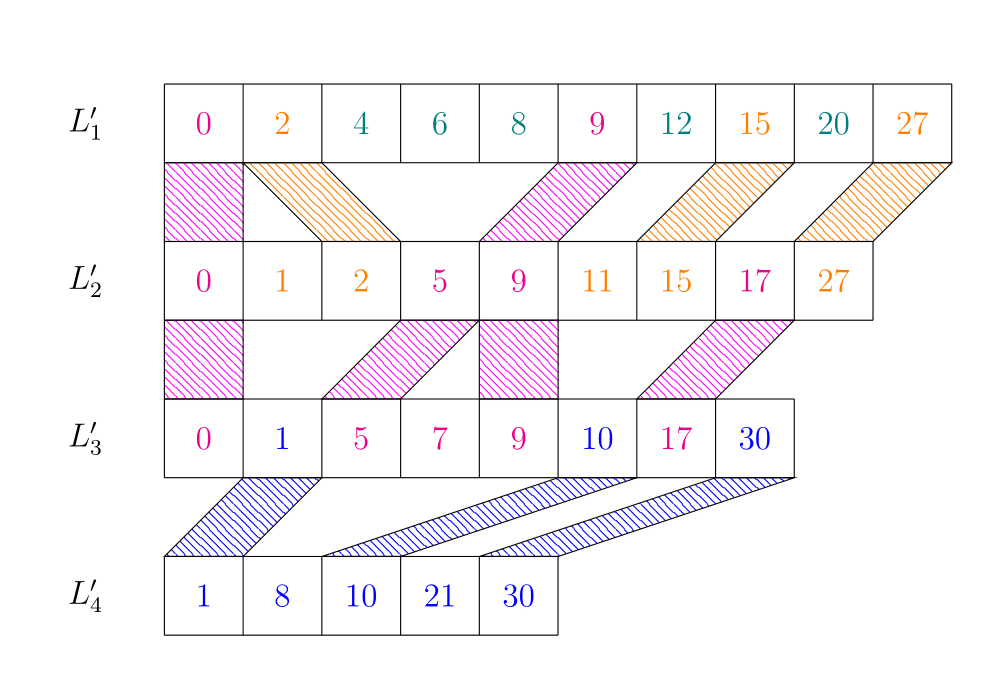Tehát az utolsó $L_4$ lista megmarad, ahogy van. Majd az $L_3$-at és az $L_4$ minden második elemét (ha $0$-tól indexelünk, akkor pl a $0$., $2$. és a $4$. indexűt) rendezve az $L'_3$ listába tesszük.

Azt tudjuk, hogy két rendezett lista összefűzése (szintén rendezett listává) $O(n)$ - azaz lineáris - idő alatt megvalósítható.

Az $L'_2$ úgy alakul ki, hogy az eredeti $L_2$ összes elemét és az újonan készített $L'_3$ minden párosadik indexű elemét bevesszük és rendezve eltároljuk. Az $L'_1$ hasonlóan. Észrevehetjük, hogy tényleg épp a duplájára nőtt az $L'_1$ mérete az eredeti mérethez képest.

Az biztos, hogy ezeket az elemeket fontos lesz "összelinkelni", tehát kelleni fog a feljebb tolt elemekből az alattuk lévő listában elfoglalt helyükre egy pointer. Meg kell jegyezzük azt is, hogy az egy eredetileg az $L_i$-ben lévő elem, vagy felkerült oda. Ennyi információ viszont még nem elég, hiszen ezzel még nem fogjuk tudni azonosítani, ha a tömbben nem szerepel a keresett érték, akkor ki is a rákövetkezője az eredeti $L_i$ tömbben, vagy ha megtaláltuk az elemet, akkor a következő listában semmi információnk nincs a helyéről!

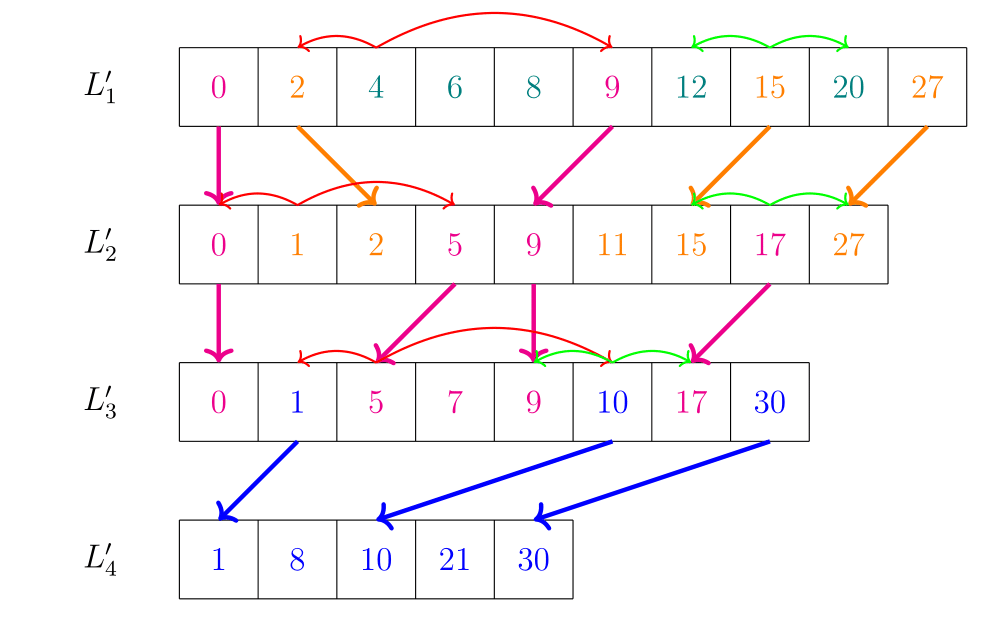
Ezt úgy javítjuk meg, hogy minden $i < k$-ra az $L'_i$ lista minden eleméből (legalább) $2$ pointerünk lesz kifele - azaz az utolsó listában szintén nem csinálunk semmit pluszban:

• ha ez az elem az eredeti $L_i$-beli, akkor a két ,,feljebb hozott'' szomszédjára mutat (pl piros nyilak)
• ha ez egy ,,feljebb hozott'' elem, akkor a két eredetileg $L_1$-ben lévő szomszédjára mutat. (pl zöld nyilak)
• ha valakit továbbítunk másik listába, azt a két elemet "linkeljük" (szám színével megegyező nyilak)

(Persze, ha csakis a rákövetkezőre van szükségünk, a megelőző elemre mutató pointereket elhagyhatjuk.)

Szóval az előző példánál maradva:

A lefelé mutató nyilak a felemelt elemek eredeti helyére mutató pointerek.

A listák eredeti elemeiből a két szomszédos alsóbb listából való elemekre mutatunk. Így például az $L'_1$ lista $4$-es eleméből mutat egy pointer a $2$ és $9$ elemekre, hiszen azokat örökölte ez a lista az $L'_2$-ből, amik a $4$-hez a rendezett listánkban a legközelebb vannak. Ez alapján tudunk a következő listában is keresni: ha maga az elem nem a keresett, akkor a rendezés miatt vagy az előtte lévő, vagy a rákövetkező lehet az. Ha egyik sem, akkor az adott elemet - ha az az eredeti $L_i$-beli - adjuk vissza, mint rákövetkező (vagy megelőző, ha arra van inkább szükség. Attól függően, melyik szomszédba mutató nyilat követjük.) Ha nem $L_i$-beli, hanem alulról kapott elem, akkor követjük az eredetire mutató pointert.

Azok az elemek, amik alsóbb listából kerültek fel, szintén két pointert kapnak, méghozzá az őket "körül vevő" eredeti listaelemekre. Például az $L'_3$-ban a $10$ az $L'_4$-ből került fel, így a két -rendezés szerint őt megelőző és rákövetkező - eredeti $L_3$-ban lévő elemre mutat belőle pointer. Azaz a $9$-be és a $17$-be.

A keresést tehát a következőképpen futtathatjuk:

• bináris keresés $L'_1$-ben. ($O(\log n)$ idő)
• ha az elem $L'_1-L_1$-ben van, akkor annak $L_1$-beli szomszédjára mutató pointert követjük, hogy megadjuk az $L_1$-beli helyét
• ha $L_1$-beli, akkor a szomszédos alsóbb listákból kapott elemekre mutató pointert követjük
• megyünk egy szinttel lejjebb

Mivel minden alsóbb listában összesen $3$ összehasonlítást kell maximum csinálnunk, kihasználva, hogy minden második elemet emeltünk fel az alsóbb listákból - hiszen vagy a feljebb tolt elem az, vagy annak valamelyik szomszédja lesz a keresett elem abban a listában. Ez pedig konstans, azaz $O(1)$ ideig tart, ezt kell $k$-szor megcsinálnunk.  Így a $k$ listában $O(k+\log n)$ az időigény.

Keressünk rá a $8$-as elemre! Ha nincs benne a listában, akkor a rendezésben rákövetkező elemet adjuk vissza!

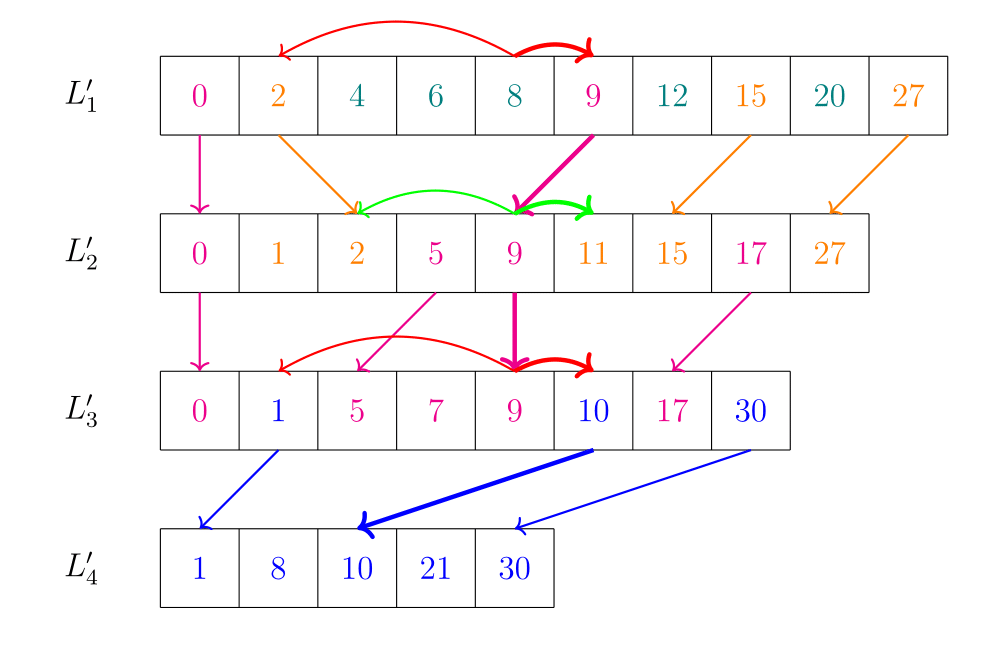
Az $L'_1$ tömbben futtatunk egy bináris keresést, ezzel pedig meg is találjuk a $8$-at a $4.$ indexen. Ez egy eredetileg is $L_1$-ben lévő elem, tehát ebben a listában vissza is adjuk a $4$-et. Ahhoz, hogy a lejjebb lévő listában lévő helyéről információt szerezzünk, kövessük a rákövetkező $L'_2$-ből kapott elemre mutató pointert. Menjünk eggyel lejjebb!

$L'_2$-ben ekkor a $9$ elemen állunk. Sem ő, sem a két mellette lévő elem nem egyezik meg a $8$-cal, így a rákövetkezőt kell visszaadjuk. Ez az elem eredetileg nem része az $L_2$-nek. Adjuk vissza a rákövetkező $L_2$-beli elemre mutató pointer által mutatott indexet (ami a $4$ lesz). Menjünk a következő szintre!

Az $L'_3$-ban szintén a $9$-en állunk. Sem ő, sem a két szomszédos elem nem a $8$! Egy $L_3$-beli rákövetkezőt kell visszaadjunk! A $9$ eredetileg is az $L_3$ része, így az ő indexét, ami szintén a $4$ adjuk vissza. Mivel eredeti listaelem, az alatta lévő listában való kereséshez az onnan örökölt szomszédját kell lefelé követnünk. Lépjünk a rákövetkező elem felé és kövessük a pointert az $L'_4$ listára.  Ebben a $10$-en állunk. Ő nem, viszont a tőle balról lévő szomszédja épp a $8$! Adjuk vissza az indexét, ami az $1$ lesz.

És kész is!

Ha érdekel a téma, Erik Demaine-től, az MIT tanárától a következő videóban hallhattok róla (56:00-69:40 között), valamint használatának egy motivációjáról egy részletesebb összefoglalót.