A feladat a következő: Adjuk meg a Fibonacci-sorozat $N.$ elemét $mod~P$, ahol $N\sim 10^9$ és $P\sim 10^6$ prím.

Ha ezt for ciklussal akarnánk megkapni, az $O(N)$ idő, ami sok. Ha $10^9$-dik Fibonacci számot ugyanennyi milliszekundum alatt tudnánk kiszámolni, még az is $11$ napig tartana, ha ugyanennyi másodperc alatt, akkor pedig kb $31$ évig. Ennyit azért nem szeretnénk várni!

Általánosan a lineáris rekurziót a következőképpen definiáljuk: \[a_{n+k+1}=c_1a_{n+1}+c_2a_{n+2}+\ldots c_ka_{n+k}\]
a $c_1,\ldots,c_k$ számok és az első $a_k$ elem az inputban adottak.

A Fibonacci sorozat esetében ezek a számok épp $a_1=a_2=1$, $c_1=c_2=1$ és $a_{n+3}=a_{n+1}+a_{n+2}$.

Az általános módszer erre az, hogy vesszük a következő mátrixot:

Ha egy $\boldsymbol{v}=(a_{n+1},a_{n+2},\ldots,a_{n+k})$ vektort megszorzunk $A$-val, akkor az eredmény $(a_{n+2},a_{n+3},\ldots,a_{n+k+1})$.

Ha ezt a feladatunkhoz szeretnénk felhasználni akkor az $N.$ Fibonacci elemet a ${(a_1,a_2,\ldots,a_k)}\cdot A^{N-k}~\% ~P$ vektor utolsó elemében kapjuk. Viszont ezt megint nem szokás így hatványozni, mert ez is sokáig tart! Ebben a sorrendben pláne nem, mert így $(N-k)$ db mátrix-vektor szorzást kell megcsinálnunk, ami $O(k^2\cdot N)$ idő.

Ahhoz, hogy egy mátrixot rövid idő alatt tudjunk hatványozni, használjuk a gyorshatványozás algoritmust (ami nagyon hasonlóan működik, mint a számok esetében):

Számoljuk ki az $A$, $A^2$, $A^4$, $A^8$, $\ldots$, $A^{2^{\lceil \log N\rceil}}$ mátrixokat előre, és tároljuk el egy számunkra szimpatikus tömbben. Majd futtassuk az algoritmust, ami így néz ki:

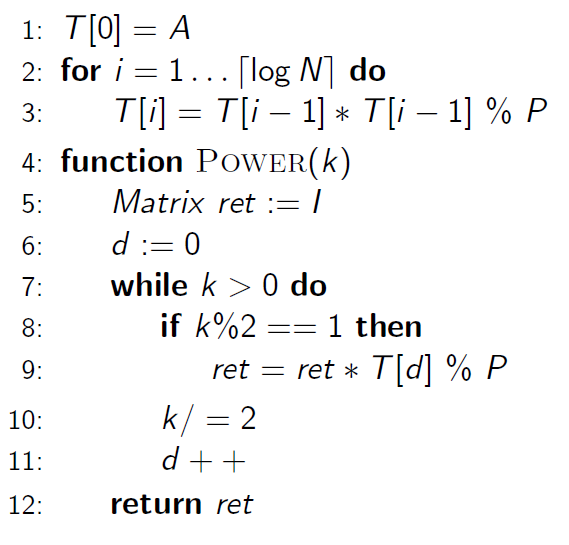Tehát inicializáláskor a T tömbbe kiszámítjuk az A megfelelő hatványait ($\mod~P$), ami összesen $\log N$ darab mátrixszorzás.

A hatványozás függvény pedig az eredménymátrixot úgy számolja ki, hogy az egységmátrixból (csak a főátlóbeli elemei $1$-ek, ez a mátrix tulajdonképpen az A nulladik hatványa) kiindulva attól függően, hogy a $k$ hatványkitevő adott bitje $1$-e beszorozzuk az aktuális $A$ hatvánnyal vagy sem. A végén tehát éppen a $k$. hatványt kapjuk vissza.

Pl: $A^13=A^1\cdot A^4\cdot A^8$, hiszen a $k=13=1101$.

Ennek az időigénye $O(k^3\log N)$, hiszen $k^3$ egy mátrixszorzás időigénye és $\log N$ idő alatt tudjuk inicializálni a $T$ tömböt, valamint hatványozásonként legfeljebb $\log N$-szer fut le a ciklusmag (mert hogy ennyi biten tudjuk ábrázolni/ennyiszer tudjuk kétfelé osztani).
(Persze mátrixszorzásra Strassen algoritmust használva, aminek $k^{\log 7}\sim k^2.8$ a futásideje, tovább javíthatjuk az algoritmust.) Mivel a $\log_2 10^9\sim 30$, így a műveleteket jelentős mértékben sikerült lefaragnunk (mondjuk az előző millisecben vett 11 napos futásidőt ezzel kb 0.2 másodpercre redukálnánk.)

A módszer ACM versenyeken kifejezetten hasznos tud lenni. Vegyük a következő feladatot:

• input: $c_1,\ldots , c_k$, $a_1,\ldots,a_k$, $m\le n$ és $P$
• output: $(a_m+\ldots+a_n)~\%~P$

Tehát a sorozat két eleme közti elemek összegét kell kiszámolnunk. Ezek persze az előzőhöz hasonlóan nagy számok lehetnek, tehát nem érünk rá kiszámolni az $m.$ elemtől az $n.$ elemig mindenkit, hogy aztán ezeket összeadjuk. Gyorsabb módszer kell!

Ekkor jön szóba a prefixösszeg számítása! Egy sorozaton belül egybefüggő intervallum összegét megkaphatjuk a következő módon:
\[S_n=a_1+\ldots+a_n~\%~P\]

Ha így számolunk, akkor pedig az $S_n-S_{m-1}~\%~P$ eredménye épp az $a_m+\dots+a_n~\%~P$.

Tehát csak ezt a két elemet kell kiszámolni. Azt pedig már tudjuk, hogy ez gyorsan megy lineáris rekurzióval és gyors mátrixhatványozással. Egy kicsit kell módosítani az algoritmuson. Az alap mátrixunk most legyen a következő:

Ekkor az $n.$ prefixösszeget az $(a_1,\ldots a_k,0)\cdot B^n$ utolsó eleme fogja adni, hiszen az utolsó oszlop mindig az adott vektor első és utolsó elemét adja össze (0-ból kiindulva pedig ez tényleg épp az $n.$ prefixösszeg lesz). Ebből kell kiszámolni kettőt, majd ezeket kivonni egymásból.

És gyorshatványozással ez is $O(k^3\log N)$ idő.