Mester Tétel
Ennek a posztnak a témája a MergeSort algoritmus időigényének meghatározása lesz, melyet hard és easy fokozaton is meg fogunk nézni. Utóbbiban megtudjuk, mi is a címben említett Mester Tétel.
Összefésülő rendezés
- Input: Egy $n$ elemet tartalmazó tömb
- Output: Az input tömb rendezve
- Algoritmus (D&C):
$MERGESORT(A[1, \ldots, n])$
- Ha $n=1\ return\ A$
- Rekurzívan alkalmazzuk a lista két felére: $MERGESORT(A[ 1, \ldots, \lceil n/2\rceil])$ és $MERGESORT(A[ \lceil n/2\rceil+1, \ldots, n ])$
- A $2$ listát ,,fésüljük össze''
Nézzünk a futására egy példát:

#theHardWay
A MergeSort időigényét egy $n$ elemű listán jelöljük $T(n)$-nel.
Vegyük sorra az algoritmus lépéseit:
- Ha a tömb egy elemű, nincs vele további dolgunk, azaz ez a művelet konstans időigényű: $T(1) =O(1)$ (Ez az eset nem túl érdekes. Mivel nincs igazán hatása a függvény időigényére, elhagyjuk)
- Meghívjuk a bal és jobb résztömbre is egyszer-egyszer a MergeSort-ot, aminek az időigénye $$T(\lceil n/2\rceil)+T(\lfloor n/2\rfloor)$$
(Viszont kihasználjuk, hogy nem tökéletesen pontos időigényt szeretnénk kiszámolni, hanem csak a függvény aszimptotikus viselkedésére vagyunk kíváncsiak, így ehelyett írhatunk annyit, hogy $2\cdot T(n/2)$!) - Ezután összefésüljük a két visszakapott rendezett listát. Mennyi ideig tart két (összesen $n$ elemet tartalmazó) rendezett lista összefésülése?

Azaz az összes elemen végig kell menjünk egyszer, páronként összehasonlítva a két lista legkisebb elemét.
Ez $O(n)$ időigény (azaz lineáris, amit szeretünk!)
Tehát eddig a rekurzív összefüggésünk: $T(n)=2\cdot T(n/2)+O(n)$
A $T(n)=2\cdot T(n/2) + cn$ egyenlet ($c>0$ konstans) rekurziós fáját (amelyben minden pont egy eljáráshívás költsége) rajzoljuk fel.
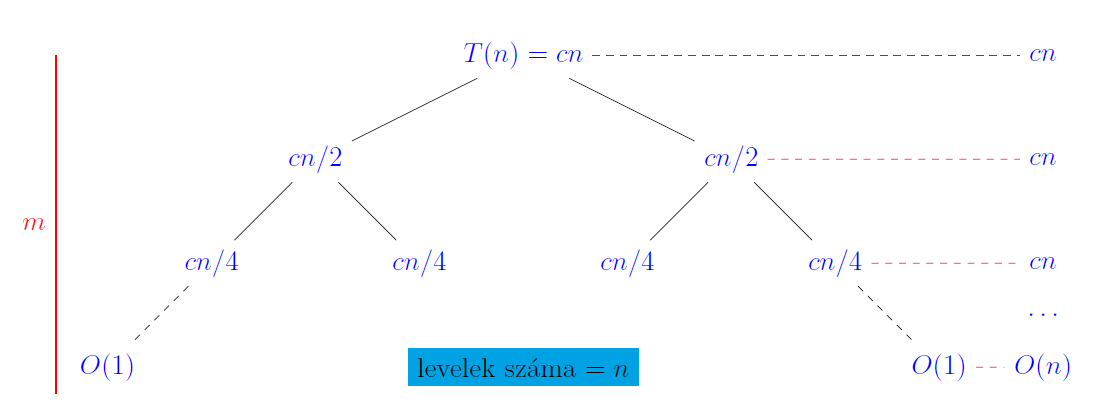
Az eljárás teljes költsége az egyes szintek költségeinek összege. Minden szint költsége $O(n)$, tehát az eljárás költsége a $m\cdot O(n)$.
Milyen magas ez a fa, mennyi az $m$? Egy tömböt addig osztunk két felé, amíg egy eleműt nem kapunk, ezt pedig már gyakorlatról is tudjuk, hogy összesen $\log n$-szer tudjuk megtenni, szóval a fa magassága $\log n$. Így az eljárás időigénye $O(n\cdot\log n)$.
Ez még könnyű volt, de egy bonyolultabb rekurzív összefüggés esetén már nincs mindig ilyen egyszerű dolgunk a rekurziós fa alapján meghatározni az időigényt. Ahhoz, hogy bonyolultabb rekurzív függvényeknek - amelyekben a részproblémák mérete megegyezik - is könnyen meg tudjuk határozni az időigényét, a Mester Tétel lesz a segítségünkre.
A Mester Tétel ,,inputja'' egy $T(n) = a \cdot T(n/b)+ O(n^d)$ alakú rekurzív összefüggés, melyben három konstans szerepel:
- $a\geq 1$ a részproblémák száma, amelyeket egy probémából készítünk
- $b>1$ egy faktor, ami azt mondja meg, hogy milyen gyorsan csökken az input mérete
- $d$ a részproblémák generálásának és a megoldásaik kombinálásához szükséges időigényben az $n$ kitevője
Továbbá specifikálnunk kell az alapeset időigényét is. Elég kicsi $n$-re (pl mikor az $n=1$), a legrosszabb eset analízis szerinti időigénye a MergeSort algoritmusnak kostans, tehát $T(n) = O(1)$.
Mester Tétel
Legyen $T(n) = a\cdot T(n/b)+ O(n^d)$ egy rekurzív összefüggés, ahol $a \geq 1$, $b > 1$. Ekkor $T(n)$-re a következő aszimptotikus korlátok adhatók.}
$$T(n) =
\begin{cases}
O(n^d \log n) &\hbox{ha }a = b^d\\
O(n^d) &\hbox{ha }a < b^d\\
O(n^{\log_b a}) &\hbox{ha }a > b^d\\
\end{cases}$$
#theEasyWay
Ha ennek segítségével szeretnénk megadni a MergeSort időigényét, először is adjuk meg a konstansokat a rekurzív összefüggésünkhöz:
- A részproblémák száma: $a=2$
- A részproblémák méretének csökkenése: (mindig a felére csökken) $b=2$
- A részproblémák eredményeinek összegzéséhez szükséges idő az összefésülés időigénye, ami $O(n)$, tehát $d=1$.
Így $2=2^1$, azaz az első eset teljesül. Az időigény: $O(n\log n)$
