Előismeret
Az irodalomjegyzékben megjelölt cikkekben Eric Kee és szerzőtársai főleg olyan módszereket vizsgáltak, amelyekkel a vetett és a mesterséges árnyékokat kísérelték meg meghatározni. A vetett árnyék (angolul cast shadow) olyan helyeken jelenik meg, amelyek valamely más tárgy által fénysugarak miatt alakul ki. A vetett árnyék geometriai szempontból egy vetítés által alakul ki, hiszen a fényforrásból induló fénysugár - mint vetítési egyenes - vetíti le a tárgy pontjait egy másik felületre. Az árnyékban lévő felület (angolul attached shadow) olyan felület részlet, amelyre nem jut fény.
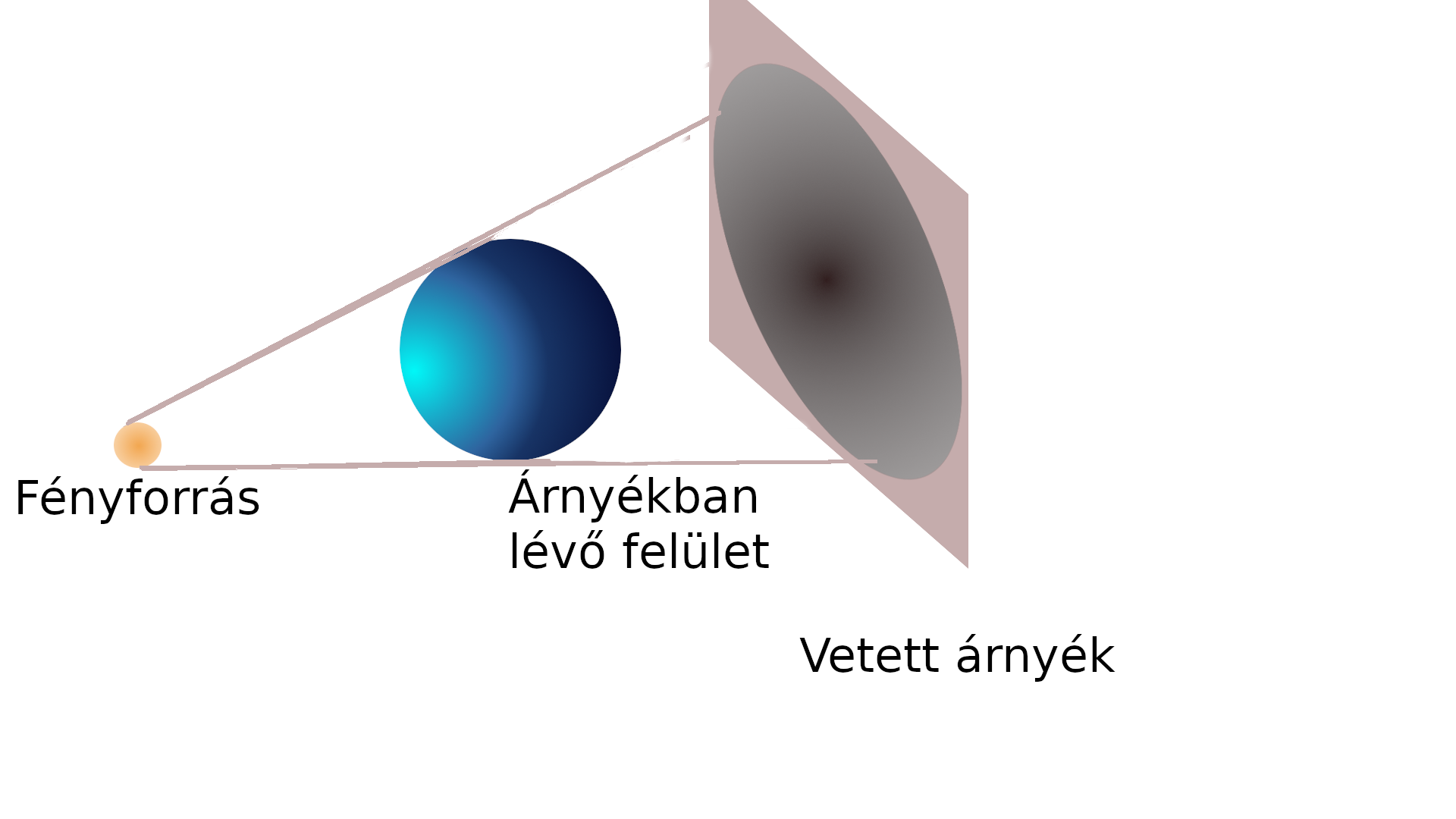
Az alábbi képen az 1-es és 2-es V-alakú részlet vetett árnyékot jelöl, míg a 3-assal jelölt félsík árnyékban lévő felülethez tartozik.

A vetett árnyékok esetében a fényforrásnak valahol a V-alakon belül kell lennie. Ez gyakran levetített objektum-sarkoknál határozható meg jól, ahol mind az árnyék sarok és jó esetben az objektum sarok is megállapítható. Ha a fényforrás a kamera mögött van, akkor a V-alakú részt 180°-kal el kell fordítani.
Az árnyékban lévő felületeknél az a vonal, ahol felületi normálvektor 90 fokot zár be a fénysugárral az árnyékban lévő felület határa.
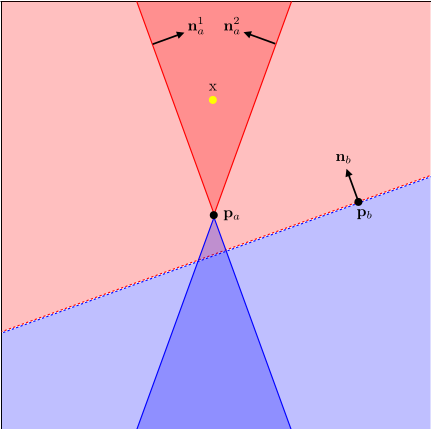
Mindkét árnyéktípus leírható egy lineáris egyenlőtlenség-rendszerrel. A V-alakú térrész két szára definiálható a normálvektoraik által valamin a pa csúcspont által.
A pb pont és az nb normálvektor által pedig az árnyékban lévő felületek félsíkjai határozhatók meg.
Formálisan egy félsík az alábbi egyenlettel definiálható:
![]()
{\mathbf{n_i} \cdot {\mathbf x} - {\mathbf n_i} \cdot {\mathbf p_i} \geq 0
ahol ni a normálvektort, pi egy egyenesen lévő pontot jelöl, x pedig a fényforrás helye.
A V-alakú térrészre az alábbi egyelőtlenség rendszerek írhatók fel:
![]()
\mathbf{n}_i^1 \cdot \mathbf{x} - \mathbf{n}_i^1 \cdot \mathbf{p}_i \geq 0 \quad \quad \mathbf{n}_i^2 \cdot \mathbf{x} - \mathbf{n}_i^2 \cdot \mathbf{p}_i \geq 0
A félsíkok és a V-alakú térrészek együttesére m darab egyenlőtlenség írható fel:
![]()
Átrendezve:
\mathbf{Nx} - \mathbf{P} \geq \mathbf{0}