Szerzők: Dr. Mingesz Róbert, Mellár János, Makan Gergely és Somogyi Anikó
Tananyag elsajátításához szükséges idő: 15 perc.
A lecke (olvasó és videólecke) bemutatja a logikai függvények kanonikus alakjainak fogalmát, ezek jelentőségét és használatuk módját. A tananyag egy rövid videóval indul, a videó tartalmának lényege pedig később szövegesen is részletezve van.
Tartalom
- Videó: A logikai függvények kanonikus alakja
- Diszjunktív normálalak
- Diszjunktív normálalak áramköri megvalósítása
- Konjunktív normálalak
Videólecke
Egy-egy logikai függvényt számos alakban lehet felírni: a kanonikus alak egy olyan egységes forma, mely egy függvényt egyértelműen egyféle módon határoz meg. Kanonikus alakból két típus van, mindegyiknek megvan a fő alkalmazási területe:
- Diszjunktív normálalak
- Konjunktív normálalak
Ítéletkalkulusban megkülönböztetik a diszjunktív normálformát és a teljes diszjunktív normálformát, digitális technikában mindig a teljes normálformákat értjük alattuk.
Diszjunktív normálalak
A diszjunktív normálalak mintermek összegéből áll: ezek olyan szorzatok, melyekben az összes független függvényváltozó szerepel, ponált vagy negált (igaz vagy tagadott) formában.
Például, 
, 
és 
változók esetén az 5. sorszámú minterm:
![\[ m_5^3=A\bar{B}C\]](http://www.inf.u-szeged.hu/~mingesz/wp-content/ql-cache/quicklatex.com-b503a1379d4c3ce2ce610a6db0b08f89_l3.png "Rendered by QuickLaTeX.com")
A minterm esetén a felső index jelöli a változók számát, az alsó index pedig a sorszámát (pl. binárisan 101). A sorszám megadásánál a változók sorrendje meghatározó, a változók sorrendjét végig meg kell tartani a feladatok megoldása során.
A diszjunktív normálalakot az igazságtáblázat alapján egyszerű felírni: ki kell választani azokat a sorokat, ahol a kimenet egyes, ezek lesznek a normálalakban szereplő mintermek. A mintermek esetén, hogy ha a változónál egyes szerepel, akkor az ponált alakban, ha nulla akkor pedig negált alakban kell beírni.
| # | | | |  |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 1 |
| 3 | 0 | 1 | 1 | 0 |
| 4 | 1 | 0 | 0 | 1 |
| 5 | 1 | 0 | 1 | 0 |
| 6 | 1 | 1 | 0 | 1 |
| 7 | 1 | 1 | 1 | 0 |
A fenti igazságtáblázatnak megfelelő kanonikus formát a következő módon tudjuk megadni:
![\[ Q=m_2^3+m_4^3+m_6^3 =\bar{A}B\bar{C}+A\bar{B}\bar{C}+AB\bar{C} =\sum^3 (2,4,6)\]](http://www.inf.u-szeged.hu/~mingesz/wp-content/ql-cache/quicklatex.com-1ff5e8d57768737d7f091359713ba869_l3.png "Rendered by QuickLaTeX.com")
Utóbbi szumma egy egyszerűsített megadási forma, amit még alkalmazni fogunk a későbbiekben.
Diszjunktív normálalak áramköri megvalósítása
A diszjunktív normálalak megvalósításához az első lépés az egyes mintermek megvalósítása. Minden minterm egy ÉS kapuból fog állni, melybe a változókat vagy ponált, vagy negált alakba kötjük be. Tehát szükségünk lesz NEM kapukra, melyek negálják a változókat. A diszjunktív normálalak a mintermek VAGY kapcsolatából áll.
Vegyük a következő függvényt: 
. A receptszerűen megvalósított kapcsolási rajz a következő ábrán látható. A példában szereplő kapcsolási mintát számos programozható logikai áramkörben is felismerhetjük.
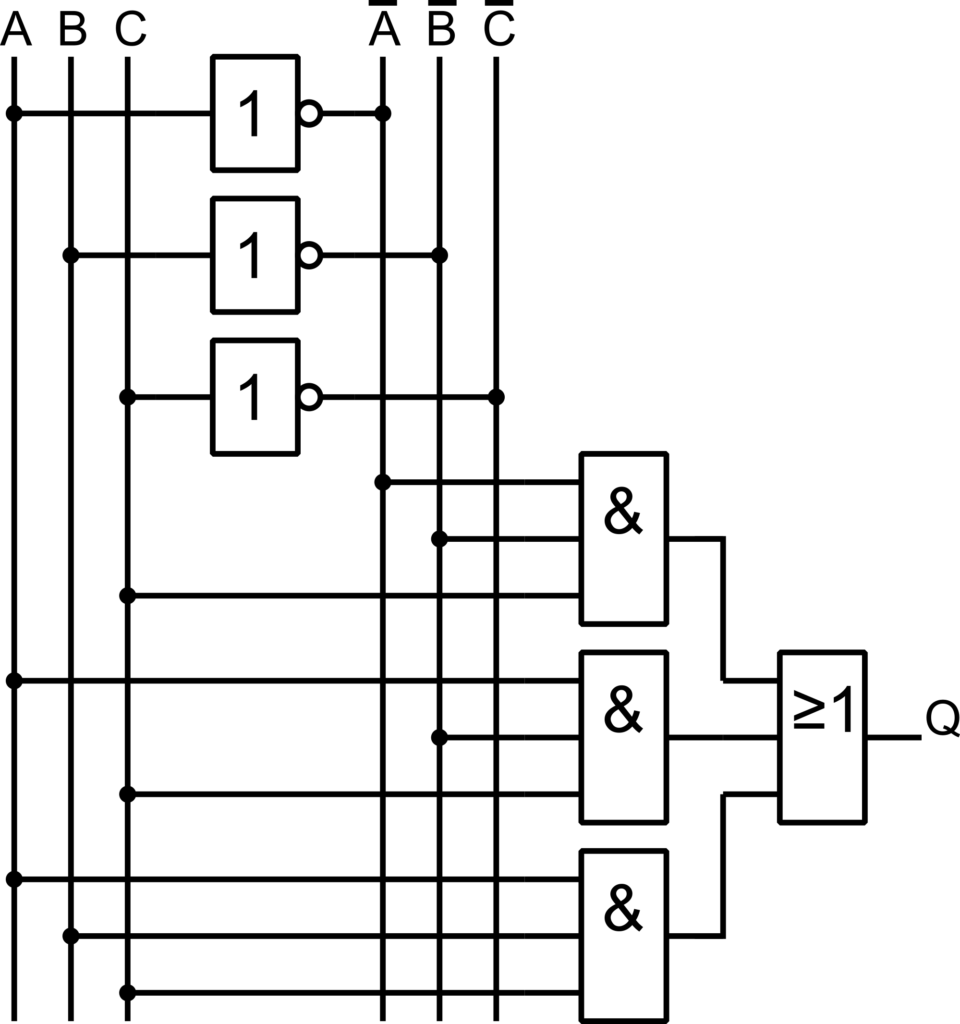
Konjunktív normálalak
Konjunktív normálalakot ritkábban használunk.
A konjunktív normálalak maxtermek szorzatából áll, a maxterm olyan összeg, mely az összes változót tartalmazza ponált vagy negált formában.
Maxtermek esetén a sorszámot a mintermhez képest eltérő módon képezzük: a ponált alakok számítanak nullának, a negált alakok pedig egynek:
![\[ M_5^3=\bar{A}+B+\bar{C}\]](http://www.inf.u-szeged.hu/~mingesz/wp-content/ql-cache/quicklatex.com-d7fdfd769d6df55c61d0bb58774c5396_l3.png "Rendered by QuickLaTeX.com")
A konjunktív normálalak igazságtáblázatból feliráísa esetén azokat a sorokat kell keresni, ahol a függvény értéke nulla. Ennek megfelelően a korábbi igazságtáblázat konjunktív normálalakja:
![\[ Q=M_7^3 \cdot M_6^3 \cdot M_4^3 \cdot M_2^3 \cdot M_0^3 =\]](http://www.inf.u-szeged.hu/~mingesz/wp-content/ql-cache/quicklatex.com-977fa7adf432041b0a64737b37c1244d_l3.png "Rendered by QuickLaTeX.com")
![\[ =\left(\bar{A}+\bar{B}+\bar{C}\right) \cdot \left(\bar{A}+\bar{B}+C\right) \cdot \left(\bar{A}+B+C\right) \cdot \left(A+\bar{B}+C\right) \cdot \left(A+B+C\right)\]](http://www.inf.u-szeged.hu/~mingesz/wp-content/ql-cache/quicklatex.com-1198190ae61b8a737999d6912c4094e1_l3.png "Rendered by QuickLaTeX.com")
Figyeljünk fel arra, hogy a számozás „fordítva” történik a diszjunktív megadáshoz képest, a maxtermek sorszáma fordított.
#1. A következők közül melyik minterm, ha a változók: A, B és C?
A minterm az összes változót tartalmazza ponált vagy negált formában, a változók között és művelet (szorzás) van.
#2. A következők közül melyik diszjunktív normálalak, ha változóink A, B és C?
A diszjunktív normálalak mintermek összege. A mintermek a változók ponált vagy negált alakjának szorzatából áll. Figyeljünk arra, hogy a külön-külön felülvonással jelölt változók, szorzata nem egyezik meg az egy közös felülvonás alatt lévő változók szorzatával. Előbbi esetén külön-külön vannak negálva a változók, utóbbi esetén a ponált változók szorzata van negálva (így a tag már nem minterm).
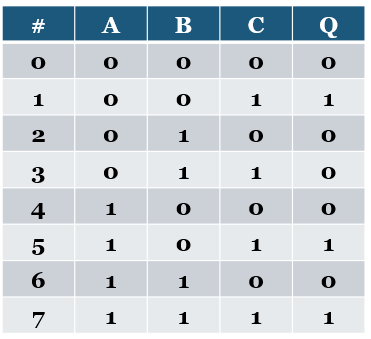
#3. A fenti igazságtáblázatnak melyik a diszjunktív normálalakja?
Két feltétel kell teljesüljön:
- A függvény legyen (teljes) diszjunktív normálalak alak
- A függvénynek azokat a mintermeket kell tartalmaznia, melyeknél a kimenet egyes
Results
Tökéletes!
További gyakorlási lehetőséget biztosít a Kanonikus alak – észrevételek és gyakorló feladatok oldal.
Van még mit javítani. Ajánljuk, hogy részletesen tanulmányozd át a Kanonikus alak – észrevételek és gyakorló feladatok oldalt.
Következő anyag: Logikai függvények egyszerűsítése Karnaugh-tábla segítségével
Digitális architektúrák tananyag | Digitális laboratóriumi gyakorlatok tananyag
Ajánlott irodalom
- David Money Harris, Sarah L. Harris: Digital Design and Computer Architecture (elérhető elektronikusan a SZTE Klebesberg Könyvtárban)
- SULiNET: A logikai függvények szabályos alakjai
Jelen tananyag a Szegedi Tudományegyetemen készült az Európai Unió támogatásával. Projekt azonosító: EFOP-3.4.3-16-2016-00014
