 Szerzők: Dr. Mingesz Róbert, Mellár János, Makan Gergely és Somogyi Anikó
Szerzők: Dr. Mingesz Róbert, Mellár János, Makan Gergely és Somogyi Anikó
Tananyag elsajátításához szükséges idő: 45 perc.
A lecke (olvasó és videólecke) bemutatja a Karnaug-táblála alapú logikai egyszerűsítés módszerét. A tananyagban számos példa látható, ez alapján el lehet sajátítani a legfontosabb lépéseket. A készségszíntű elsajátításhoz érdemes példákat megoldani, így mélyítve el a tudást. A tananyag egy rövid videóval indul, a videó tartalmának lényege pedig később szövegesen is részletezve van.
Tartalom
- Videó: Logikai függvények egyszerűsítése Karnaugh-tábla segítségével
- Példa algebrai egyszerűsítésre
- A Karnaugh-tábla használata függvények egyszerűsítésére
- Speciális esetek kezelése
Videólecke
Olvasólecke
Logikai függvények egyszerűsítésére egy módszer az algebrai egyszerűsítés. Itt a Boole-algebra azonosságait felhasználva alakítjuk át a függvényeket azon célból, hogy kevesebb tagból álljon a felírás vagy egyszerűbb legyen a fizikai megvalósítás.
Példa algebrai egyszerűsítésre
| # | ||||
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 1 |
| 3 | 0 | 1 | 1 | 0 |
| 4 | 1 | 0 | 0 | 1 |
| 5 | 1 | 0 | 1 | 0 |
| 6 | 1 | 1 | 0 | 1 |
| 7 | 1 | 1 | 1 | 0 |
A fenti igazságtáblázatnak megfelelő függvény egyszerűsítésének lehetséges lépései:
1) Kiinduló állapot a diszjunktív normálalak:![]()
2) Az utolsó tagot megkettőzzük az „![]() ” azonosságnak megfelelően:
” azonosságnak megfelelően:![]()
3) Az egyenletet átrendezzük a kommutativitás szabályának megfelelően:![]()
4) A disztribbutivitás azonosságát felhasználva:![]()
5) Az „![]() ” azonosság alapján:
” azonosság alapján:![]()
6) Utolsó lépésként kiemeljük ![]() -t, és átrendezzük az
-t, és átrendezzük az ![]() és
és ![]() tagot:
tagot:![]()
Az algebrai egyszerűsítések kivitelezése komoly odafigyelést és gyakorlatot igényel, ezért számos olyan módszer létezik, melyek valamilyen szempontból egyszerűbbé vagy automatizálhatóvá teszik az egyszerűsítés menetét. A következőben bemutatott Karnaugh-táblás módszer, valamint a Quine- McCluskey eljárás a fenti egyszerűsítés 1-5 pontját alkalmazza a háttérben, ezt a részletet érdemes megjegyezni, mivel így egyszerűbb lesz a módszerek megértése.
A Karnaugh-tábla használata függvények egyszerűsítésére
A Karnaugh-tábla olyan grafikus egyszerűsítési módszer, mely négy változói egyszerűen alkalmazható. Magasabb változószám esetén ritkán alkalmazzák. A Karnaugh-tábla felírásakor a változók sorrendje tetszőleges, azonban a táblázat felírása egyszerűbb, hogy ha az igazságtáblázatban megadott sorrendet követjük.
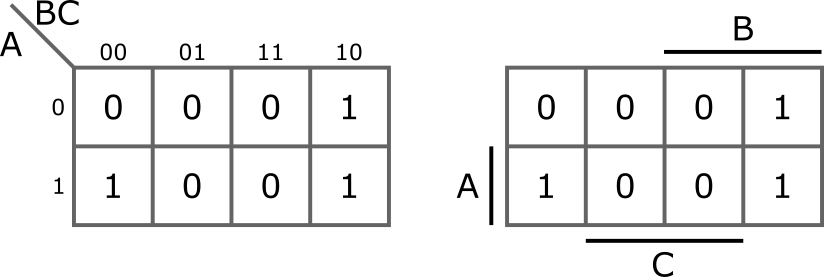
A Karnaugh-tábla megértésében segít, hogy ha beírjuk a minterm sorszámát, vagy akár az adott mintermhez tartozó biteket (lásd következő ábra). Hogy ha megnézzük az oszlopokat, feltűnik, hogy az utolsó két oszlop fel van cserélve. Így, az összes egymás melletti oszlop csak egy változóban különbözik egymástól.
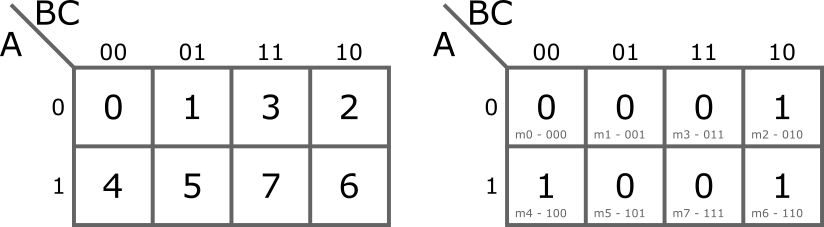
Az egyszerűsítés során a táblában olyan tömböket jelölünk ki, melyek kettő hatványa számú egyest tartalmaznak (pl. 1, 2, 4, 8). Az összes egyest le kell fedni legalább egyszer, 0-kat pedig nem szabad lefedni. A tábla szélén lévő cellák szomszédosak a túloldalon lévő cellákkal. Egy-egy egyest tartalmazó minterm akár többször is felhasználható.
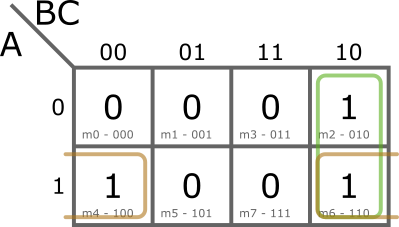
Hogy ha a fenti ábrát részletesen megfigyeljük, észrevehetjük, hogy az m6-os mintermet kétszer is felhasználtuk, hasonlóan az algebrai egyszerűsítés 2) lépéséhez. Az m2-es és m6-os a következő miatt vonható össze:
![]()
Az ![]() változó, mely a kijelölt tömb mentén különböző értékeket vehet fel, kiesik. Az m4 és m6-os mintermek hasonló módon vonhatok össze:
változó, mely a kijelölt tömb mentén különböző értékeket vehet fel, kiesik. Az m4 és m6-os mintermek hasonló módon vonhatok össze:
![]()
Ebben az esetben a ![]() változó esik ki. A fenti példa alapján látható, hogy az egyszerűsítés módszere lényegében megfelel a korábban bemutatott algebrai egyszerűsítés 2)-5) lépéseinek. A később tárgyalt Quine- McCluskey módszer is ugyanezt követi. Az utolsó két oszlop cseréjét is érthetjük ez alapján: a cél az, hogy egy-egy szomszédos cella (minterm) csak egy változóban különbözhessen, így azokat össze lehessen vonni.
változó esik ki. A fenti példa alapján látható, hogy az egyszerűsítés módszere lényegében megfelel a korábban bemutatott algebrai egyszerűsítés 2)-5) lépéseinek. A később tárgyalt Quine- McCluskey módszer is ugyanezt követi. Az utolsó két oszlop cseréjét is érthetjük ez alapján: a cél az, hogy egy-egy szomszédos cella (minterm) csak egy változóban különbözhessen, így azokat össze lehessen vonni.
Az egyszerűsítés utolsó lépése, a Karnaugh-tábla alapján felírni a primimplikánsokat tartalmazó algebrai alakot, ahol minden egyest tartalmazó mintermet legalább egyszer lefedtünk, de nincsenek benne „felesleges” tömbök. Az egyes tagok felírása egyszerű: minden olyan változó, melynek értéke változik a tömbön belül kiesik.
![]()
A kapott függvény nem feltétlenül a legegyszerűbb alak (kiemelhető a ![]() ). Ez nem minden esetben jelent problémát, van, amikor ennek az alaknak az áramköri megvalósítása a legegyszerűbb.
). Ez nem minden esetben jelent problémát, van, amikor ennek az alaknak az áramköri megvalósítása a legegyszerűbb.
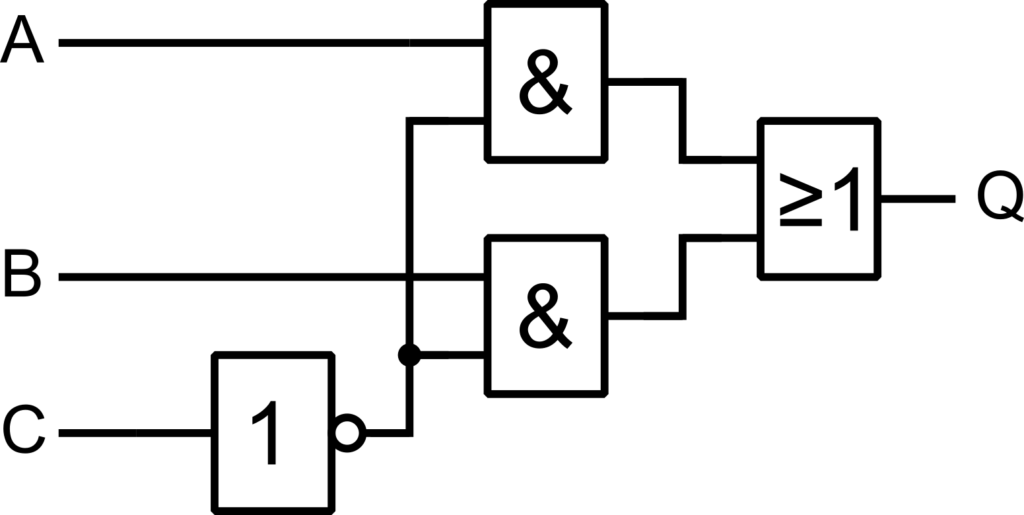
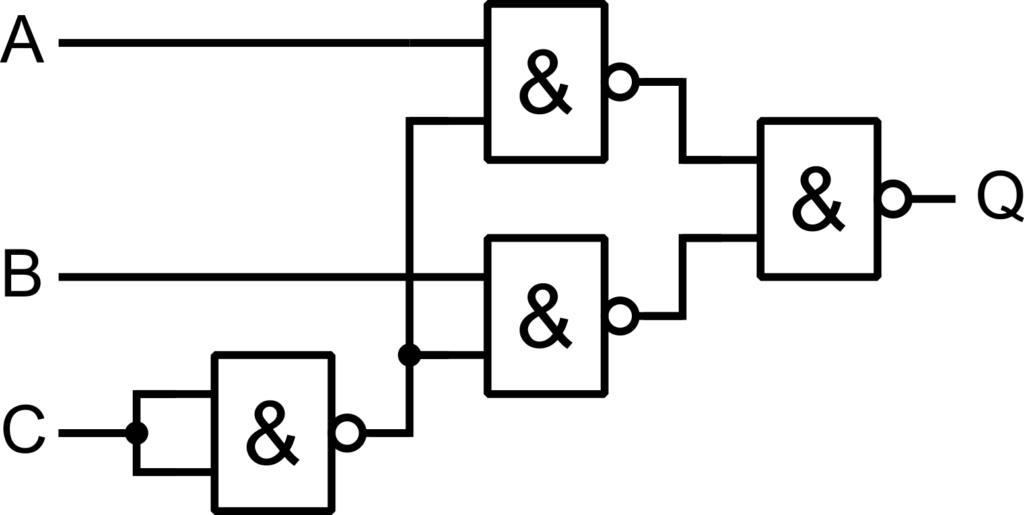
A fenti ábrán látható, hogy hogyan lehet megvalósítani a végeredményként kapott függvényt logikai kapukkal. A kapcsolás három fajta logikai kaput igényel. A De-Morgan azonosságoknak megfelelően, azonban a VAGY kaput helyettesíthetjük ÉS kapuval is, amennyiben a bemeneteket és a kimeneteket is negáljuk. Az ennek megfelelő, egyszerűsített végeredménye a következő ábrán látható.
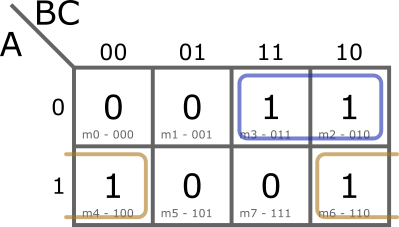
Vegyük a következő példát: ![]()
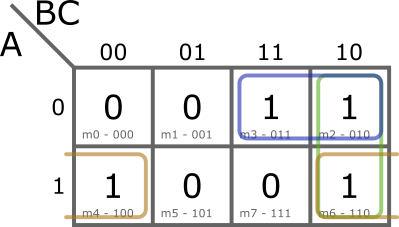
Az egyszerűsítés eredménye: ![]() . Figyeljük meg, hogy az ábrán zölddel jelölt implikáns olyan mintermeket fed le, melyeket a másik kettő is lefed, a tag redundáns. Így ez a tag elhagyható, a végeredmény egyszerűbb lesz:
. Figyeljük meg, hogy az ábrán zölddel jelölt implikáns olyan mintermeket fed le, melyeket a másik kettő is lefed, a tag redundáns. Így ez a tag elhagyható, a végeredmény egyszerűbb lesz: ![]() .
.
A Karnaugh tábla négy változó esetén 4×4-es méretű lesz. Itt az utolsó két oszlop van megcserélve, ennek oka szintén az, hogy így a szomszédos mintermek csak egyetlen változóban térnek el. Szintén két módszer terjedt el a változók jelölésére (Karnaugh- és Veitch-féle), a feladatok megoldásánál bármelyik használható.
Példaként tekintsük a következő függvényt: ![]() .
.
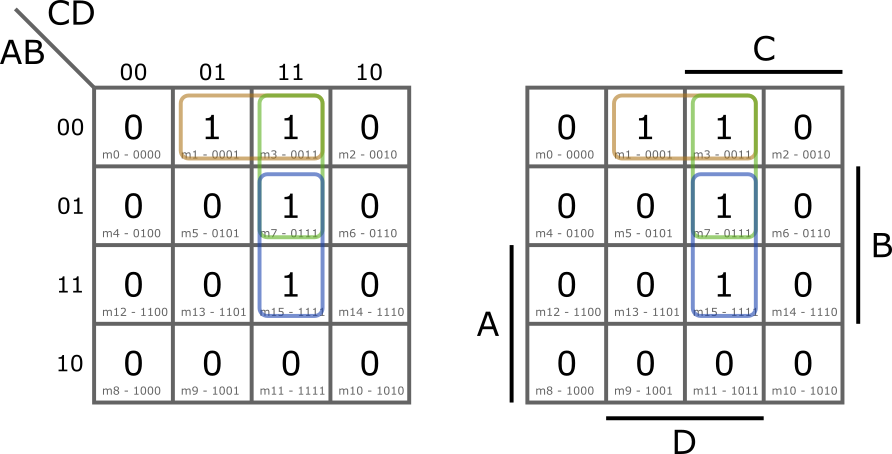
Az egyszerűsítés eredménye: ![]() . Az utolsó, az ábrán zölddel jelölt tag redundáns, így elhagyható.
. Az utolsó, az ábrán zölddel jelölt tag redundáns, így elhagyható.
A Karnaugh táblában a 0 jelöléseket gyakran elhagyjuk, gyorsítva az eljárást. A következő példában is ezt követjük. A példában láthatjuk, hogy mindig a legnagyobb egybefüggő, kettő hatványú mintermet tartalmazó implikánsokat keressük, jelen esetben egyetlen egyet.
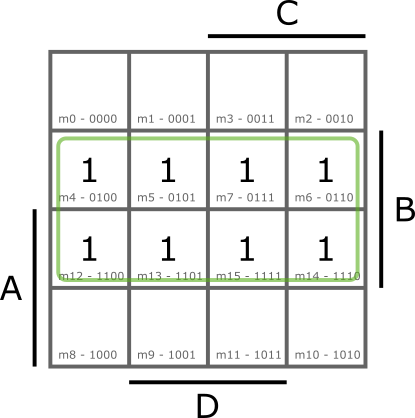
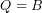
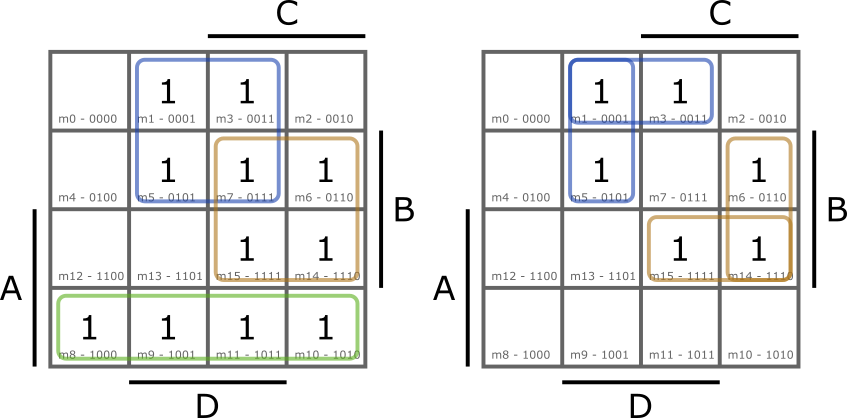
A tábla szélein lévő mintermek, illetve a sarkon lévő mintermek is egymással szomszédosak, ahogy a következő két példában lehet látni.
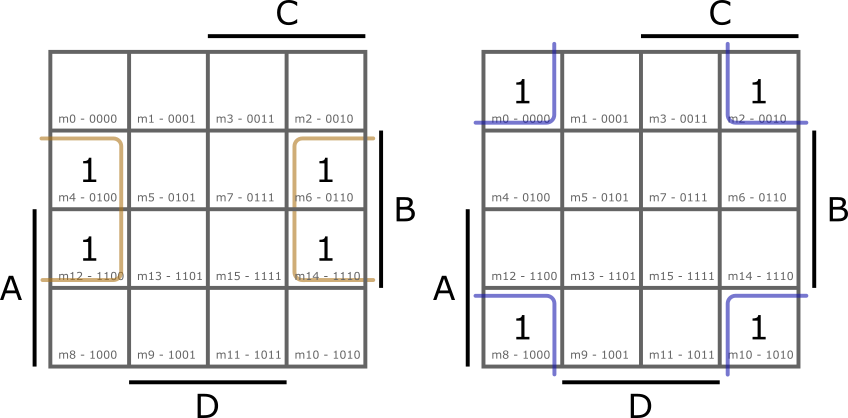
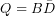 , a jobboldali:
, a jobboldali: 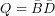
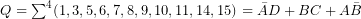
Jobbra:
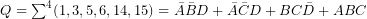
Vannak olyan esetek, amikor valamilyen okból, adott bemeneti kombináció mellett nem határozzuk meg a kimenet értékét (közömbös kombinációk, don’t care). Ezeket a sorokat X-el jelöljük mind az igazságtáblázatban, mind pedig a Karnaugh-táblában. Summával kifejezett algebrai alak esetén ezeket a mintermeket általában ![]() -vel jelöljük:
-vel jelöljük: ![]()
Az egyszerűsítés során szabadon eldönthetjük, hogy a táblában X-el jelölt, közömbös kombinációkat bevesszük-e a tömbök kialakításába, vagy nem. A cél mindig az, hogy a legegyszerűbb végeredményt kapjuk:
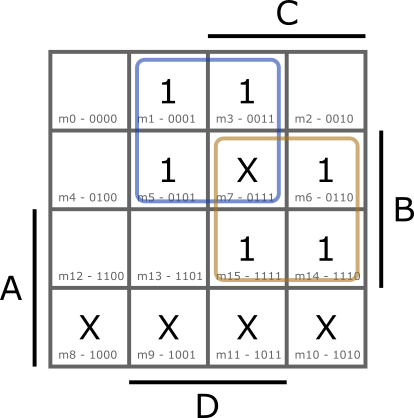
Az egyszerűsítés során a 7. mintermet figyelembe vesszük, a 8-11-es mintermeket viszont nem. A végeredmény: ![]() . Hasonlítsuk össze a végeredményt azzal, mint amikor az összes X helyén egyes van, vagy az összes X helyén nulla van (lásd korábban).
. Hasonlítsuk össze a végeredményt azzal, mint amikor az összes X helyén egyes van, vagy az összes X helyén nulla van (lásd korábban).
Összefoglalva az egyes lépéseket:
1. lépés
A Karnaugh táblában egyest írunk be azon mintermek helyésre, ahol az igazságtáblázatban is egyes szerepel.
2. lépés
A karnaugh táblában megkeressük a lehetséges legnagyobb implikánsokat. Az implikánsok kettő hatvány darab mintermet tartalmazhatnak. Az összes egyest legalább egyszer bekarikázzuk.
3. lépés
Megkeressük a redundáns implikánsokat, ezek kihagyhatók a végeredményből
4. lépés
Felirjuk a végeredményt függvény alakjában. Szükség esetén felrajzoljuk a függvényt megvalósító kapcsolási rajzot.
#1. Az alábbiak közül melyik helyesen kiválasztott implikáns?
Csak az egyessel jelölt mintermek fedhetők le (vagy ha van közömbös kombináció, akkor azok).
Csak kettő hatvány darab minterm fedhető le.
Mindig a legnagyobb lefedést keressük.
#2. Melyik tábla felel meg az fenti képletnek?
Figyelni kell arra, hogy az utolsó két oszlop meg van cserélve. Ezen felül a negált alakok oda kerülnek, ahol az adott változó értéke 0, a ponált alakok pedig oda, ahol a változó értéke 1.
#3. Melyik végeredmény felel meg az fenti függvénynek?
Ugyanez az egyenlet volt a korábbi feladatban is. Két implikánst kell bekarikázni, a jobb oldalon lévő négyest, és a két alsó sarkot. Ezt követően meg kell állapítani, hogy milyen függvények felelnek meg a kiválasztott implikánsoknak: azon változók kiesnek, melyek az implikánsban nem konstansok. Ahol a változó értéke nulla, a változó negált alakban fog szerepelni, ahol egy, ott a változó ponált alakban fog szerepelni.
Results
Ez jól sikerült!
Van még mit javítani.
Előző anyag: Logikai függvények kanonikus alakja
Digitális architektúrák tananyag | Digitális laboratóriumi gyakorlatok tananyag
Ajánlott irodalom
- Matijevics István: Digitális technika példatár, Typotex Kiadó, 2011, elérhető: Digitális tankönyvtár.
- Interaktív program Matijevics István példatárához:
http://www.inf.u-szeged.hu/projectdirs/digipeldatar/digitalis_peldatar.html
(A program használata a flash bővítmény engedélyezését igényli) - David Money Harris, Sarah L. Harris: Digital Design and Computer Architecture (elérhető elektronikusan a SZTE Klebesberg Könyvtárban)
- SULiNET: A logikai függvények szabályos alakjai
Jelen tananyag a Szegedi Tudományegyetemen készült az Európai Unió támogatásával. Projekt azonosító: EFOP-3.4.3-16-2016-00014
