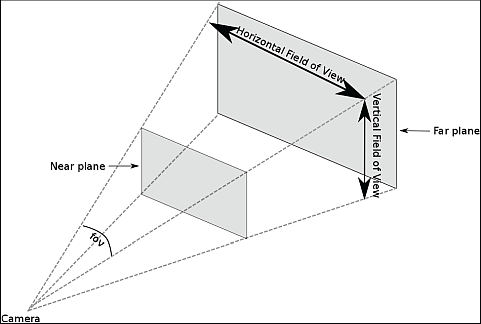
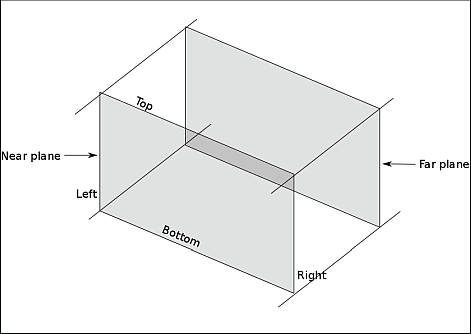
A Three.js magasszintű API-ja részekre bontja a kamera nézet beállítását. Alacsonyabb szinten jellemzően a szintén lookAt() vagy hasonló nevű nevű függvényt hívjuk három darab háromelemű vektorral, vagy 9 darab számértékkel az alábbiak szerint:
- eye_x, eye_y, eye_z: a kamera középpont térbeli elhelyezkedése (ez a Three.js position attribútuma),
- target_x, target_y, target_z: a kamera vetítési célpontjának megadására (ezt a térbeli pontot adhatjuk meg a Three.js lookAt() függvényével),
- up_x, up_y, up_z: a kamera nézeti felfelé irányának megadására (ez a Three.js up attribútuma).
Az alacsonyszintű lookAt() függvény egy 4x4 méretű mátrixot ad, amit a ModelView mátrix View komponenseként használhatunk fel. (Ennek részleteivel most nem foglalkozunk.) Az előző fejezetben tárgyalt object.matrix is rendelkezik lookAt() függvénnyel.
A koncepció lényegét az alábbi ábra magyarázza el.
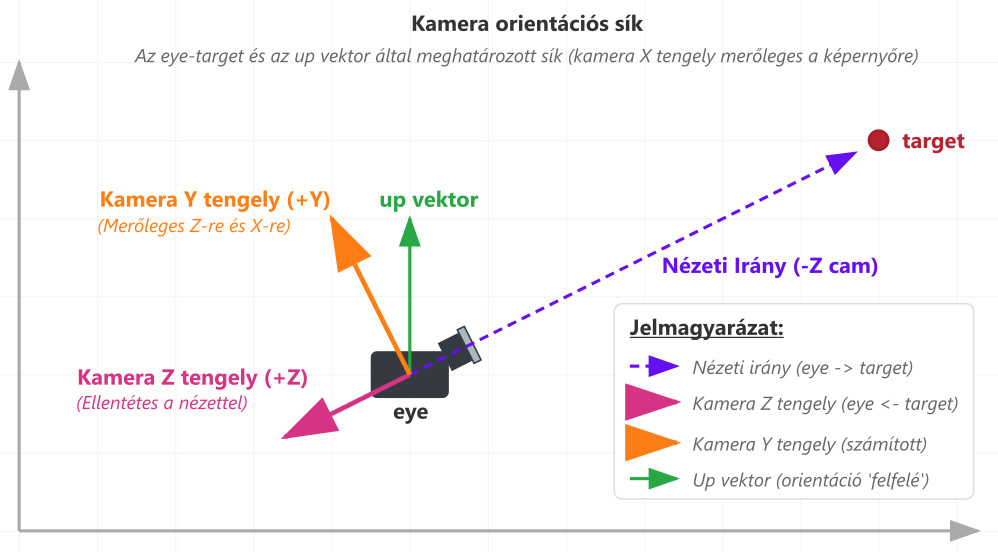
Az ábra a térbeli világ XYZ koordináta-rendszer azon síkját mutatja, amelyet az eye → target és az up vektor irányok feszítenek ki. (Ha ezek egymással párhuzamos irányt adnak, akkor baj van, lásd később.)
A kamera nézeti irányát az eye és a target térbeli koordináták által definiált vektor adja. Az OpenGL (és így WebGL és Three.js) használati mód szerint az alapértelmezett kamera a negatív Z-tengely irányba néz, így a kamera koordináta-rendszer Z-tengelye ezzel ellentétes irányú lesz.
A kamera X-tengely irányát az up vektor és az eye → target vektor keresztszorzata adja. (Figyeljünk arra, hogy a keresztszorzat nem kommutatív művelet, vagyis a tényezők sorrendje nem cserélhető fel.) A keresztszorzat eredménye egy új vektor lesz, aminek az iránya az előző két vektor által kifeszített síkra merőleges lesz. Hosszát egység méretre kell alakítani, normalizálni kell. Ezt a vektor koordináták vektor hosszal való osztásával érhetjük el. Jobbsodrású koordináta-rendszer lévén a fenti ábrán ez a képernyő síkjából felénk kifelé mutató kamera X-tengely irányt jelent.
Vegyük észre, hogy a kamera koordináta-rendszer Y-tengely irányát általános esetben nem az általunk megadott up vektor fogja adni. Az up vektor csak egy nézeti orientációt jelent, ami nem kell merőleges legyen az eye → target vektorra. A kamera Y-tengelyének viszont ilyennek kell lenni. Ezt egy újabb keresztszorzattal kapjuk a már meglévő kamera Z és X- tengely irányokat használva.
Bár komplikáltabbnak tűnhet, a valós életbeli kamera forgatásokat ezzel a paraméterezéssel kényelmesebben meg tudjuk adni.
Néhány dolog, amire figyeljünk modellezéskor.
- Ha a kamera célpontja mozog, akkor az új koordinátáit minden megjelenítő (render) ciklusban meg kell adni a kamera objektumnak.
- Vigyázzunk arra, hogy az up vektor és az eye → target vektor ne legyen egymással párhuzamos. Ilyen esetben a keresztszorzatuk nullvektort ad, ami nem értelmezhető térbeli irányként. Orientációs szabadsági fokot vesztünk, ahogy az előző fejezetben a gimbal lock tárgyalásakor láttuk.
- Az objektum geometriai transzformációs attribútumokkal ellentétben a kamera nézeti beállításokat rögzített sorrendben kell végrehajtanunk a kódban! Először adjuk meg a két attribútumot (position és up) tetszőleges sorrendben, és csak ezek után hívjuk a lookAt() függvényt! Ennek oka, hogy a lookAt() függvény hívásakor a Three.js rögtön kiszámítja a nézeti orientációt reprezentáló egység kvaterniót, az nem a renderer.render() függvény végrehajtásakor történik!
A 4x4 méretű View mátrix számítása két lépésből áll. Azt szeretnénk elérni, hogy a kamera az általános térbeli elhelyezkedéséből és orientációjából a normalizált helyzetbe kerüljön: a (0, 0, 0) térbeli pozícióból a negatív Z-tengely irányba nézzen. Ehhez először eltolást kell alkalmazni az eye koordináták negatív értékével (így kerül a szem az origóba):
T = \left( \begin{matrix} 1 & 0 & 0 & -eye_x \\ 0 & 1 & 0 & -eye_y \\ 0 & 0 & 1 & -eye_z \\ 0 & 0 & 0 & 1 \end{matrix} \right)
Következő lépésként a forgatást kell alaphelyzetbe állítanunk. A koordináta-rendszer váltást a mátrix oszlopokban elhelyezett új X, Y és Z normalizált (egységnyi hosszúságú térbeli vektorral megadott) bázis irányok megadásával érhetjük el. Viszont itt egy már meglévő általános orientációból térünk vissza a világ X, Y és Z irányaihoz, vagyis a fordított, inverz forgatásra van szükségünk. Egy 3x3-as forgató mátrix inverze a mátrix transzponáltjával egyenlő. Vagyis a 4x4-es transzformációs mátrixunk felső 3x3-as forgató részmátrixának soraiba kell beírnunk a kamera X, Y és Z tengelyek normalizált irányvektorait:
R = \left( \begin{matrix} X_x & X_y & X_z & 0 \\ Y_x & Y_y & Y_z & 0 \\ Z_x & Z_y & Z_z & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right)
A View mátrix a két mátrix szorzataként adódik: